|
| Question |
|
Topic | Doug's Commentary |
| "How does quantum~nonlocality affect Aristotle's syllogisms?" | Early December, 2010 - Massachusetts | Quantum~Nonlocality and classical propositional logic. |
Almost all quantum phenomena affect all classical logical constructs. When Doug uses "affect" here his hermeneutic is quantumism is "adversely affective on classicism." Quantum locality~nonlocality memes are good exemplars of quantum adverse affects on classical logic. Over simply quantum~reality is dynamic. Compare that to classical logics' dependence on classical state. All classical logics are analytic, and analyticity depends upon state, at least motional stoppability. Quantum~reality has n¤ state, n¤r is it classically stoppable. Locality vav nonlocality viewed classically depend, further, upon a classical notion of 'position.' Classicists assume 'position' may be 'determined' state-ically. In quantum~reality this is simply impossible due absolute motion and change of quantum~reality itself. In quantum~reality there are n¤ classical "zero-motion reference frames." So we have to remove any classical notion of position from our descriptions of quantum l¤cality~n¤nl¤cality. We have similar issues with classical context vav quantum comtext. Classicists assume 'context' is same everywhere, i.e., "one global context." If you thinkq about this, you will see this violates a quantum~meme of general holographicity in quantum~reality. Classicists assume badly that local and nonlocal share a single classical context. Quantumists assert that l¤cal and n¤nl¤cal comtexts may never be classically identical. Classicists assume badly that local and nonlocal have state. Quantumists assert that n¤ island in quantum~reality and n¤ ensemble of islands have classical state, due absolute quantum~flux. So quantum~n¤nl¤cality denies any validity of Aristotle's syllogisms. Doug - 8Dec2010. |
|
|
|||
An Aristotle Connection
Aristotle's approach, given his excellent foundation, was totally rational: based upon a presumed objective existence of substance. Aristotle's assumption gave us his famous subject-object schism. Objects are rationally real. Subjects are unreal (~irrational). All of classical Western science prior to quantum physics is based upon Aristotle's schism!
Well, now we know that schism is wrong! It is a façade.
Logical Laws of a Great Sophism Hater, Aristotle:
Aristotle gave us his three laws of propositional logic (used for syllogistic thinking):
|
(Text quote revisions in response to a visitor's comments; 14-16Mar2002 - Doug.) All Aristotle quotes above from The Great Books, Volume 8, Aristotle I. These lists are partial. Many "as used" occurrences of all three tautologies appear repeatedly in Aristotle's works. It is important at this juncture to realize that Aristotle's syllogisms deny quantum reality. As such they are only valid within his own contrived substantial, material, objective axiomatic mythos. They are generally invalid in quantum reality and in quantum logic. See Jammer's Quantum Logic. See Foulis' Quantum Logic. Sophists whom Aristotle denigrated were much closer to intuiting quantum reality than Aristotle ever was. Good Examples are Heraclitus, Anaxagoras, and apparently Protagoras whom he refutes above. Socrates was executed for his quantum sophism. Zeno, co-founder of an Eleatic school with Parmenides appears to us more as a sophist, while Parmenides appears wholly Aristotelian. Bottom line:
Aristotle fed modern Western Culture a bill of goods, a deign
of classical feign. Aristotle's contrived classical reality does
n¤t 'exist!' For an example of Aristotle's quantum-inept classical thing-king see our comments on what some folk call "Aristotle's natural state model." |
Now, what assumptions are these laws based upon?
They are based upon an assumed classical subject-object schism. Classical thought's schism assumes objects exist, objects are substantial, and objects do not change or cohere any other objects or phenomena. It assumes subjective is insubstantial, and does not exist for purposes of objective syllogistic thinking.
So, what did Aristotle assume about 'A' in his laws above? He assumed 'A' represents something real. He assumed 'A' exists. Therefore 'A' must stand for something which exists. 'A' must stand for a real object.
Are there any implicit assumptions in Aristotle's three laws of logic? What about his first law? It says A=A. That is a tautology. In other words, classically it is always true. His syllogism, A=A, is an absolute truth according to Aristotle.
In addition, explicitly, Aristotle assumed what 'A' stands-for/represents must be real. So A=A is an absolute truth, and 'A' is real.
And what do we know about absolute truth? Absolute truth is both complete and consistent. Complete means: states all truths. Consistent means: always states the truth. A=A is just a proposition, so it need not state all truths, but it does need to be consistent. So does A=A always state the truth? We can deny an assumption of classical objective reality, and we can deny an assumption that A=A is consistent. If our denials are correct, we can state with certainty that A=A does not always state the truth.
What do we know for sure today about real objects in a classical macro world? No two classical objects of similar categories are identical (e.g., snowflakes, hemoglobin molecules, diamond crystals, zebra, corn, pennies, water molecules, etc. See The Sciences, Sep/Oct 1997 issue, 'Tiny Doubles,' by Hans Christian von Baeyer, pp. 11-13) No two classical real objects, in general, can possibly be identical to one another.
So, we surmise, Aristotle tells us that an object is identical to itself. We would ask, "When?" When is an object identical to itself? Now, we know every classically real object in a real multiverse may changæ, however subtly, at least as fast as Planck's frequency, or about 1043 times per unit spatial reference. So every classical real object is different from itself, in general, more frequently than Planck's multiversal quantum rate. (Change time base reference to space based reference. 16Mar2002 - Doug.)
There is no A separate from itself that is identical to itself in a classical real world! Practically speaking, there is no A identical to itself in a classical real world! Quantum reality denies both interpretations of Aristotle's first law of syllogistic logic.
What about Aristotle's second law? It says, "A must be either A or not A." We can treat it similarly to his third law, discussed just below: "A issi both A and c¤mplement-A." See issi.
Recall our parenthetical above: (See Aristotle's Metaphysics, 'Further Refutation of Protagoras' - . [1011b-13]: "(1) ...that the most indisputable of all beliefs is that contradictory statements are not at the same time true...") Quantonics students, adept O'gadons, notice here what Pirsig noticed about Einstein, Aristotle is assuming that 'truth' is a 'function' of time. Doug - 1Aug2006.
We can say, both "There 'is' fighting in the world," and we can say "There 'is' 'not' fighting in the world," and both contradictory statements are classically 'true' simultaneously, almost always. So Aristotle's indisputable is rather simply disputed, and we did it classically too, without having to invoke quantum reality assumptions!
Aristotle assumed OGC and OGT. Quantum reality shows us that both quantum~comtextings and quantum~truthings are, among other classically-heterodoxical and -heretical paralogisms, animate and heterogeneous. See coquecigrues.
Doug - 6Mar2006.
What about Aristotle's third law? It says, "A cannot be both A and not A." This is another classical objective assumption, not a law! Again Aristotle's subject-object schism is a problem here. Aristotelian reality composes only of real substance, real objects. There is no insubstantial reality in Aristotelian reality.
But now we know a better, n¤vel reality is quantum reality which subsumes classical reality. What Aristotle called real objects are only partial objects. A quantum equivalent is like our model shown in Figure 5, of our Quantum Connections text. In quantum reality we refer A issi both A and c¤mplement-A as a quantum~included~middle. Quantum flux can and does quantum c¤mplementarily middle~include other quantum flux. Doug - 6Mar2006. Using quantum logic to restate Aristotle's third law, we say, "A is both A and n¤t A." In quantum reality, a better reality, A is both its actual part and its quantum~middle~included n¤nactual c¤mplement. (For a more complex, more recent, July, 2002, example see our Quantonic Ensehmble Quantum Interrelationships.) Also see our How to Become A Student of Quantonics discussion on classical excluded-middle vis-à-vis quantum~included~middle.
What other implicit assumptions did Aristotle make? Are there any assumptions that might shock him if he were aware that he had made them? Yes!
Just above, we pointed out that Aristotle, like Einstein, assumed that 'truth' is a function of time. But he made other more 'gross' and opinionated classical assumptions too. Doug - 1Aug2006.
Remember our title for this section, apropos our review of Buridan's work? 'The Logical Laws of a great sophism hater, Aristotle.' What else did he assume about his three laws? He assumed they are tautologies. Why? Because he assumed they are self-referent and always true! If Aristotle were right here today, able to do discourse with us, do you think he would be surprised to learn that self-referent tautologies which are paradoxical and thus contextually inconsistent (and thus, according to Buridan, contradictory) are sophisms?
Aristotle, a great hater of sophisms, founded his logic on sophisms! Allow your reviewer to show Aristotle's laws again interpreted in quantum reality, but perceived classically as paradice:
| • a law of identity - (A is A) | — in quantum reality A issi both A and n¤t A, |
| • a law of contradiction - (A must be either A or not A) | — in quantum reality A issi both A and n¤t A, |
| • a law of an excluded middle - (A cannot be both A and not A) | — in quantum reality A issi both A and n¤t A. |
So, thinking SOM classically, we can now see Aristotle's three laws, given (presuming) a more general quantum reality, are each self-referent and paradoxical!
In classical reality, a tautology is self-referent and always true. In classical reality a sophism is self-referent and always paradoxical and thus inconsistent (and thus false according to Buridan). However, in quantum reality we replace Aristotle's three laws with one statement, "A is both A and n¤t A." That statement, in general quantum reality is true. To retain Aristotle's laws, one must presume his contrived-for-convenience, simplistic, incomplete SOM world.
We must conclude Aristotelian logic, and all formal logics founded on it are n¤t logics which deal with reality, but are logics of very restricted conventional contexts within a much larger quantum reality. Further, any logic based upon an existence of classical substantial objects is n¤t a logic about reality, but is a logic of a very restricted, anthropocentric, conventional context within a more general quantum reality.
Aside:
Assumptions (like Aristotle's list of syllogisms, or axioms, rules, laws, corollaries, lemmas, etc.) serve to define subsets of larger reality. A good way to imagine a set of axioms or rules is one of several metaphors:
- a box,
- a limited contextual trap, or
- a local logical prison. (Note: each of these metaphors is innately n¤nabsolute — each metaphor may be locally consistent, but always is globally/multiversally incomplete.)
"Rules and axioms are fences which classically bind and confine quantum-inseparable pieces of reality."
Then imagine reality's actual part as an unlimited set of boxes, traps, or logical prisons — each with its own set of local axioms. Each metaphor (Kuhnian paradigmatically) describes SOM. It is just one small part of actual reality. Aristotle's reality is just one small actual piece of reality.
Where SOM sees inconsistency in sophisms, MoQ and quantum science see opportunity. SOM's malperceived "false" sophisms vis-à-vis sophisms' inconsistency are carte blanche quantum tells.
By comparison MoQ and quantum science both describe all known and unknown actual parts of reality and assume an unknown, undefinable part of reality.
What did we just say? What is this both known and unknown, both definable and undefinable stuff? For review, let's take another quick look at a more quantum model of reality:
Our reality model is open, infinite, massively parallel, omnimensional, discontinuous quantum loops:
|
(Our original table was prepared as you see it above during 1999. Since then, we have adopted our own heuristic that quantum reality may be grammatically expressed as an animate, heterogeneous, emergent, present participle reality. We should read 'model' as 'modelings,' 'loops' as 'loopings,' 'measure' as 'measurings,' 'changæ' as 'changings,' 'commingle' as 'comminglings,' etc. We choose, just now, for legacy and pedagogical reasons to retain our legacy grammar, while hoping that students of Quantonics can see how our own heuristics evolve as we grow our quantum stages.)
Mathematicians presume their assumptions are context free (i.e., they assume OGT [one global truth system] in OGC [one global context]). But now we can see their assumptions (any finite, consistent but incomplete axiom set) are not context free, but instead form or define a local context. Too, their ill-considered but innocent use of ideal objective symbols traps them in a limited context. Also, mathematicians make unstated and locally convenient assumptions (most often regarding their own perceived Platonic, non-physical reality) which elicit inevitable contradictions and concomitant paradice. Perhaps worse, exhibiting declining integrity of a noble discipline, their assumptions appear to elicit unique explanations (calls to Platonic spirits?) for paradice emersion (e.g., C is the set of all sets).
Perhaps Western science's most famous call to Platonic spirits is Einstein's 'hidden variables' explanation of quantum science's n¤nlocal affects on probabilistic local measurements of a system. Einstein, essentially an Aristotelian legacy classicist, trapped himself in his own OGT/OGC prison, and showed his predicament to all other scientists via his lame claim of 'hidden variables.' Today, we would just say simply that Einstein did not understand quantum reality's intrinsic nature as absolute flux.
Reinterpreting, we can now (late 2004) say absolute quantum flux is what Einstein misperceived — using his classical, local, naïve interpretation of reality — as "hidden variables." Doug - 24Oct2004.
Begin note:
We refer Einstein's call to spirits "lame" here since we assume he assumed OGT in OGC (we assume he was a SOMite). His call is lame to us in his inability to deny a closed OGT in OGC (I.e., his inability to deny SOM's innate incompleteness due to analyticity, closure, etc. And also, his innate inconsistency borne of affects of non-SOM contexts on his closed SOM's presumption of OGC. Those affects induce what classicists like Einstein call "sophisms and paradoxes," and we call "paradice." Those innate incapabilities and his worship in SOM's closed church of reason blinded him to ever seeing quantum reality's many islands of truth many/most of which 'reside' outside of SOM's OGT.). Had he allowed larger, open and plural quantum context(s) of contexts, his 'hidden variables' might then have appeared to him as qualitative quantum affects from outside his cherished SOM box. Einstein denied any existence of 'aether,' science's then equivalent of VES, based upon famous Michelson-Morley experiments.See Edward Williams Morley: "American chemist and physicist who with Albert Michelson disproved the existence of aether, the hypothetical medium of electromagnetic waves."
The American Heritage® Dictionary of the English Language, Third Edition copyright © 1992 by Houghton Mifflin Company. Electronic version licensed from InfoSoft International, Inc. All rights reserved.
Michelson and Morley, in ~1887, determined an "absence of aether drift" which was interpreted as a classical scientific refutation of aether's presence in reality. (Later (1948), Casimir showed existence of quantum vacuum flux, a physical dual concept to 'aether.') Einstein depended on nonexistence of aether and Michelson's Nobel Prize winning (1907) interferometer experiments which showed light's velocity constant in all 'inertial' frames. Einstein's theories of special relativity depended on Michelson-Morley results. Einstein went on to replace 'ether' with his 3D reference frame plus a fourth time dimension. Minkowski depicted Einstein's 4D as real and imaginary space and time. He never was able to 'fix' his reference frame in his model of classical reality. His general relativity made such an absolute dimensional reference fixation unnecessary.
Our Quantonic version of modern quantum science depends upon VES as a dual of Pirsig's DQ.
Again, reinterpreting, we can now (late 2004) say Michelson and Morley were just plain wrong in their 'proof' of "absence of aether drift." We have shown that we can measure absolute motion. See this text segment in our Quantum Pendulum. Doug - 24Oct2004.
End note.Note what Einstein did. He informed a set of local assumptions. His assumptions put him in an intrinsically incomplete box. Incorrectly and innately, he further assumed his box complete. Our example of Einstein's last assumption illustrates a classical OGT/OGC assumption which classicists, almost with religious fervor, have made since Parmenides, Socrates, Plato, and Aristotle.
Further, mathematicians depend upon Aristotle's syllogistic concepts (syllogistic laws 1-3 shown above) to prove or disprove theorems. Most frequently you hear them say a proof fails because an axiom leads to a 'contradiction.' This is hugely interesting. Note how mathematicians perceive 'contradiction' as failure. From a MoQ philosophical or quantum science perspective 'contradiction' is not failure, not disproof, but opportunity. Contradiction does not mean failure. It means your efforts to prove an axiom of your theory have taken you out of your local box/trap/prison.
A great example in classical mathematics is 2 + 2 = 4. It can never be anything else. Why? Because mathematics' classical box/trap/prison/convention/rules say so. A most important goal any mathematician has is proof, and in order to prove anything, s-he must stay in a rigorous community-imposed convention. (And what does Quantonics teach us about all closed conventions? That they are always multiversally both inconsistent and incomplete! Evidence? Gödel's Incompleteness Theorems. Quantum Umcærtainty. Our work here in Quantonics. Etc.)
But opportunity exists to jump out of prison and expand one's mathematical horizons. We can say 2 + 2 = 5 when we enlarge our convention to allow an other context (we have to admit mathematics is innately (by design) and intrinsically (naturally) context dependent instead of context free) which just adds one (i.e., + 1) to other contexts with which it has interrelationships under selected (possibly formerly unknown) conditions.
Hmmm...context free? Doug, what do you mean by that? What most mathematicians mean is a convention which works generally for all contexts. I.e., a context for all contexts. This is akin OGT and OGC. But what are we hearing now all over again...C is the set of all sets...context free is the set of all contexts...hmmm... Sounds suspiciously like Aristotle's syllogisms all over again, doesn't it? Perceived classically, 'context free' is a sophism (I.e., it is none, one, either/or all depending on your need/convenience to explain what you mean, thus self-contradictory even from a classical perspective.). 'Context free' is a sophism just like Aristotle's syllogisms. I ask you, why do mathematicians continue to make this enormous mistake in rational judgment? We surmise their box is limited, they refuse to admit it, and they sweep ill-fitting results under mathematics' magic carpet whose appellations variously are, "absurd, unreasonable, chimeric, subjective, etc." Ah, 'tis but a human condition. Classical physicists, et al., do too.
A new dawn will brighten mathematical vistas when mathematicians intuit MoQ philosophy and quantum science. Please, we beg you, arise soon dawn, show us philo-sophy, show us love of-sophisms, show us love of-many truths. Free us from our monoboxed, static, one-logic-fits-all troglodytic fear of change. Shine many truths' light in our hubristic caves of condescension.
So we can see now that 2 + 2 = 4 is a fact only in a local context where axioms demand it. In a similar fashion we can say that pXm (p times m) is always equal to mXp in our same conventional local context. So what do we do when we discover pXm does not equal mXp in our carefully contrived local context? Mired in convention, classical scientists and mathematicians discard enormous opportunity and say, "Impossible. Absurd. Unreasonable." And today, near our second millennium's end, we know pXm does not equal mXp (i.e., n¤ncommutativity of Poisson's bracket) in quantum reality. We know classical mathematics' Aristotelian syllogistic-based axioms, OGT and OGC are too limited. They cannot express, "Impossible. Absurd. Unreasonable," general facts about larger quantum reality. Clearly to a classical mind the solution is to declare quantum science, "Incomplete, unusable, a sophism." (That is what Einstein said about quantum science (9Jul2002 - Doug: see our recently completed review of EPR). He was so persistent at this, he ended up embarrassing himself and his associates as told by Dr. Gerald Holton in a recent issue of Physics Today. 14Aug2000 Doug.)
But guess what? Duphous classical scientists and theoreticians have boldly proceeded with inherent classical limitations and assumed they could:
- Automate classical proofs (Yes, yes, I know...our Quantonics web site links to a quantum logic site at MIT where they do this...hmmm...beware!)
- Verify and validate trusted classical computing systems (our US government paid moocho dinero for this futile effort)
- Classically automate grammars (Chomsky, Hofstadter, Chalmers, et al., still believe it possible!)
All above within Aristotle's classical prison. Can't do it, period, i.e., not if you want it to work in general reality.
So, again, we state some not-so-obvious. Rather than a single, classical, Aristotelian global context/truth, there are an infinity of conventions, an infinity of contexts. We call these, "many truths." Do you want to prove a truth in any one of these contexts? And you want to use formal logic? Then, assume a local convention and context . State your assumptions about your chosen context. Consider any possible unstated assumptions. Recognize that your results are unique to your chosen context. Your results cannot be general! Recognize your results are intended to be unique to your chosen local context, but n¤n-classical reality subsumes any context. Therefore your results are not absolute! Larger reality subsumes them, regardless, making them n¤nabsolute.
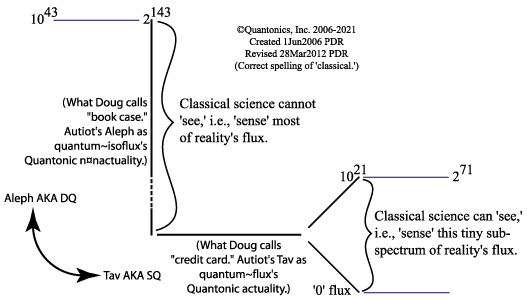
Your results are by necessity, simultaneously both inconsistent and incomplete:
| Results are: | in a smaller context: | in a larger context: |
| both inconsistent | more consistent | less consistent |
| and incomplete | less complete | more complete |
I.e., never absolute! Gödel showed us this in his Incompleteness Theorems.
And there is more to offer here in some not-so-obvious. Buridan wanted to use quasi-Aristotelian dialectical formal logic to eliminate paradoxes (paradice), especially any paradice in his revered sophisms. Once you adopt a Pirsigean/quantum reality of many truths, you adopt a great tool against paradice. Many paradice arise from an interpretation of two or more truth-contexts in an assumed Aristotelian SOM classical objective single global truth context. Any liar paradox is one example. Any Galilean integer-squares correspondence paradox is another. In a sense SOM, as Pirsig told us, manufactures paradice. In a similar sense, many truths eliminates paradice!
But you say, "I want to do proofs in a context of general
reality." Well just hope, for a future, when you may use
new memes, logics, i.e., coquecigrues,
quantum~mathematics, symbols, i.e., quantum~semiotics, quantum~memeotics,
and quantum~heuristics~hermeneutics based on many truths and quantum
objects or their successors, i.e., quantons.
There is a distinct possibility you may hope indefinitely. In
an interim, do your proofs in local, well-defined con(m)texts,
and realize your local contexts are in general comtextual
reality and general comtextual reality is in
your local contexts. Red text updates by Doug - 2Jun2006.
Afterthought:
Our own personal exposition of Aristotle's sophist laws brings great delight! We see a primitive, but great mind deny vigorously what he calls sophistry, yet uses sophistry unwittingly himself! We might use this new knowledge to denigrate Aristotle. No! As we have said elsewhere in this review, Aristotle would have called quantum science, "Sophistry, or a sophism." He would say he hates sophism as not objective, and you could not prove any absolute truth logically within any sophist realm. And he would be right! Reality is not objective. Reality offers no absolute truth!
We know now, given quantum science, reality is self-referent. Reality is omnicomtextual. Reality is n¤t one great context envisioned by Aristotle's primitive mind. Reality is a grand sophism! It is n¤t one great domain of truth in which formal logic may assess absolute truth! Reality is many emerging quasi-truths in infinite quantonic interrelationships with infinitely many other emerging quasi-truths.
Thanks for reading,
Doug.
Definition - Innate: Here, we mean a classical concept as axiomatic to a philosophy. A concept is designed in, anthropocentrically, as philosophical genetic code. (SOM appeals to humanism and anthropocentrism.)
Definition - Intrinsic: Here, we mean a comcept/meme as natural, part of an underlying reality which its philosophy attempts to describe. (MoQ appeals to an unknown, an undifferentiated (quantum isocohesive) isoflux isocontinuum, a n¤nactuality, a n¤napparent n¤nphysical space (e.g., Vacuum Energy Space, Quantum Vacuum Flux, Zero Point Flux/Energy, etc.), something greater than itself.)
ReturnReturn to Hughes-Buridan Book Review