|
Our approach follows a line of classical reasoning like this:
Assume stochastics
- that no two physical (i.e., actual) coherent
quantum comtexts'
chaos~equilibria interrelationshipings are evolutionarily comsistent
out of a group of 'n' energy~wellings in 't' total possible energy~wellings,
and
- that no two physical (i.e., actual) decoherent
quantum comtexts'
chaos~equilibria interrelationshipings are evolutionarily comsistent
out of a group of 'n' energy~wellings in 't' total possible energy~wellings
is, S(n,t)=t!/((t-n)! * tn).
Then we assume stochastics
- that two or more physical quantum comtexts are more equilibrial and less chaotic
out of a group of 'n' coherent
energy~wellings, and
- that two or more physical quantum comtexts are more chaotic and less equilibrial
out of a group of 'n' decoherent
energy~wellings
is, P(n,t) = 1 - S(n,t).
We approximated our calculation of S(n,t) using (1-n/(2*d))n-1
Classical Problematics (need wingdings font for our fickle
quantum fingers :):
 Analyticity (determinism, induction, cause-effect, homogeneous
time or independent variable as change, axiom of independence
(a strict derivation of Aristotle's
3rd syllogistic 'law,' claiming excluded-middle 'independence'
of classical objects), et al.) -
Analyticity (determinism, induction, cause-effect, homogeneous
time or independent variable as change, axiom of independence
(a strict derivation of Aristotle's
3rd syllogistic 'law,' claiming excluded-middle 'independence'
of classical objects), et al.) -
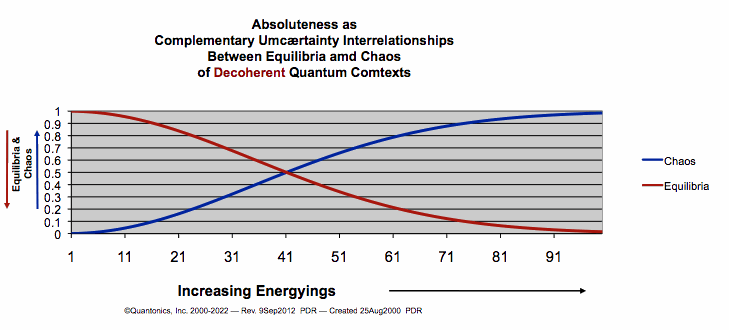
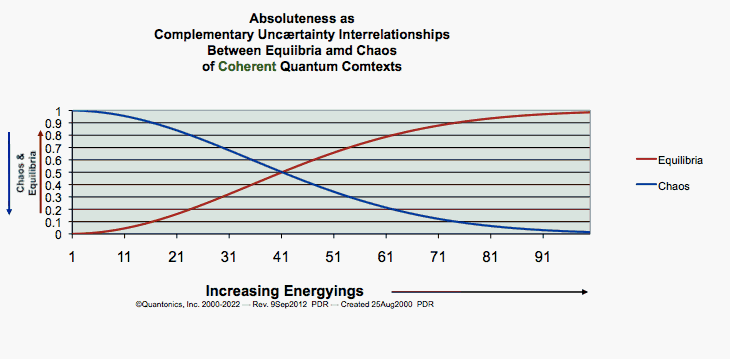
- As you can see in our graphs above and our classical equations,
a classical assumption of monism as continuous and unitemporal
(from a purely classical-ideal "reality is stoppable"
view...atemporal)
analyticity is inherent. Our classical equation is continuous.

- But is reality analytic? N¤!
Reality is quantal,
as graph just above illustrates. Here is an exemplar:
- Do our continuous, analytic
stochastic graphs of our probability~plausibility~likelihood
functions for classical equilibria
and chaos depict quantal
reality? N¤! However, we benefit
from making these classical comparisons, since they show us chaoequil interrelationshipings vary with coherent~decoherent
quantum~comtextings. If this makes you thinkq of PBings(cohera,decohera)
and PBings(equilibria,chaos), Doug has achieved a partial quantum~affectation. Also, these two graphics illustrate a great
quantum tell: quantum~reality is complementary. Complementarity
appears ubiquitous and perpetual in all quantum~reality at all
scales of quantum~reality. Chaos complements equilibrium and vice versa. Coherence complements decoherence and vice versa. Latter
is an essential of quantum~evolutionary~creation processings
as exhibited in both QED and QCD, and other omnisciplines like Bohm's Hologramic~Quantum~Theory, Bergson's Creation Philosophy, Quantonics, Qabala, and its associated cosmic energy language:
Autiot, etc. Doug - 10Sep2012.
 Localability, isolability/individuicity, separability, and reducibility
(lisr) -
Localability, isolability/individuicity, separability, and reducibility
(lisr) -
- A classical assumption of lisr is inherent in classical reasoning.
- Each classical context is lisr.
- Each classical context adheres Aristotelian syllogisms,
especially objective, excluded-middles among all classical contexts.
- But is reality lisr? N¤! Reality is quantum c¤hesive.
- Do our continuous, analytic
graphs of our probability functions for classical equilibria and chaos
depict quantum c¤hesive reality? Yæs,
partially! They show quanton(chaos,equilibrium) as quantum~complementary and thus, to some
extent, quantum~coherent due an Quantonics assumption of quantum~middle~inclusion.
Ditto quanton(coherence,decoherence). Trouble is, those analytic
graphs do it using classical maths' canonic Aristotelian sillygisms!
 Ideal mathematical integer constancy -
Ideal mathematical integer constancy -
- A classical assumption that an ideal logical/physical constant,
one (1), exists.
- A classical assumption that ideal logical/physical manipulations
of one (1) exist:
- 1/1 iso 1
- 1*1 iso 1
- 1+1 iso 2 (inference of induction and counting)
- 1-1 iso 0 (inherent definition of zero)
- 1 = 1 iso classical ideal identity
- d1/dt = 0 (1st derivative of a 'constant' is zero; assumes
homogeneous time)
- (1-1)/(1-1) iso undefined (Isn't this amazing?)
- But does reality generate or manifest physical integer constants?
N¤! All quantum n¤mbærs
are umcærtain! N¤ tw¤ quantum n¤mbærs
are identical! Too, they are perpetually
and ubiquitously evolving. In general it is n¤t
p¤ssible f¤r tw¤ quantum n¤mbærs
t¤ be physically and thus l¤gically identical.
- Do our continuous, analytic
graphs of our probability functions for classical equilibria and chaos
depict quantum n¤mbær umcærtainty? N¤!
(I.e., classical use of '1-P.')
Quantum~n¤mbærs are dynamic,
evolving processings. For example, see Doug's Quantum~Hamiltonian.
- See Doug's list of Suggested
Requirements for A New Quantum~Mathematics.
So, reader, you can see how classical concepts,
especially classical mathematical sillygistic
concepts, impede any real
and natural understanding of quantum~reality. N¤
mathematician ever shows '1' as a quantum umcærtain comcept.
(Using n¤vel
memes presented here we can d¤ that.)
F¤r ¤ur purp¤ses here, let's assume that
¤ur least values f¤r equilibria
and chaos in ¤ur n¤nclassical,
quantum~reality are individual quanta. Our curves d¤ n¤t
sh¤w that; h¤wever, we can imagine their classical
zero asymptotes as
reality's minimum Planck quantum, i.e., quantum_2•quantum_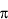 •h. •h.
|