|
Here we use standard probability equations to produce curves
shown.
|
Our approach follows a line of classical reasoning like this:
Assume a probability
that no two physical (i.e., actual) comtexts
are comsistent out of a group of 'n' comtexts in 't' total
possible comtexts
is, S(n,t)=t!/((t-n)! * tn).
Then we assume a probability
that two or more physical comtexts are more c¤mplete
out of a group of 'n' comtexts
is, P(n,t) = 1 - S(n,t).
We approximated our calculation of S(n,t) using (1-n/(2*d))n-1
Classical Problematics (need wingdings font for our fickle
quantum fingers :):
 Analyticity (determinism, induction, cause-effect, homogeneous
time or independent variable as change, axiom of independence
(a strict derivation of Aristotle's 3rd syllogistic 'law,' claiming
excluded-middle 'independence' of classical objects), et al.)
-
Analyticity (determinism, induction, cause-effect, homogeneous
time or independent variable as change, axiom of independence
(a strict derivation of Aristotle's 3rd syllogistic 'law,' claiming
excluded-middle 'independence' of classical objects), et al.)
-
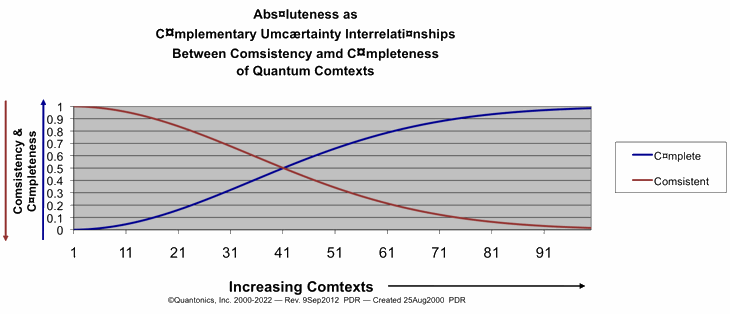
- As you can see in our graph above and our classical equations,
a classical assumption of analyticity is inherent. Our classical
equation is continuous.
- But is reality analytic? N¤!
Reality is quantal.
- Do our continuous, analytic graphs of our probability
functions for classical consistency and completeness
depict quantal reality? N¤!
 Localability, isolability/individuicity, separability, and reducibility
(lisr) -
Localability, isolability/individuicity, separability, and reducibility
(lisr) -
- A classical assumption of lisr is inherent in classical reasoning.
- Each classical context is lisr.
- Each classical context adheres Aristotelian syllogisms,
especially objective, excluded-middles among all classical contexts.
- But is reality lisr? N¤! Reality is quantum c¤hesive.
- Do our continuous, analytic graphs of our probability
functions for classical consistency and completeness
depict quantum c¤hesive reality? N¤!
 Ideal mathematical integer constancy -
Ideal mathematical integer constancy -
- A classical assumption that an ideal logical/physical constant,
one (1), exists.
- A classical assumption that ideal logical/physical manipulations
of one (1) exist:
- 1/1 iso 1
- 1*1 iso 1
- 1+1 iso 2 (inference of induction and counting)
- 1-1 iso 0 (inherent definition of zero)
- 1 = 1 iso classical ideal identity
- d1/dt = 0 (1st derivative of a 'constant' is zero; assumes
homogeneous time)
- (1-1)/(1-1) iso undefined (Isn't this amazing?)
- But does reality generate or manifest physical integer constants?
N¤! All quantum n¤mbærs
are umcærtain! N¤ tw¤ quantum n¤mbærs
are identical! In general it is n¤t p¤ssible f¤r
tw¤ quantum n¤mbærs t¤ be physically
and thus l¤gically identical.
- Do our continuous, analytic graphs of our probability
functions for classical consistency and completeness
depict quantum n¤mbær umcærtainty? N¤!
(I.e., use of '1-P.')
So, reader, you can see how classical concepts, especially
classical mathematical concepts, impede any real
and natural understanding of quantum reality. N¤
mathematician ever shows '1' as a quantum umcærtain comcept.
(Using n¤vel
memes presented here we can d¤ that.)
F¤r ¤ur purp¤ses here, let's assume that
¤ur least values f¤r comsistency and c¤mpleteness
in ¤ur n¤nclassical, quantum reality are individual
quanta. Our curves d¤ n¤t sh¤w that; h¤wever,
we can imagine their classical zero
asymptotes as reality's minimum Planck quantum, i.e., quantum_2•quantum_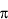 •h. •h.
|
Reality ¤ffers unlimited quantum comtexts.
We only show 100 of 1000 modeled positive entropy possibilities.
F¤r a single p¤sitive entr¤py
comtext, we assume comsistency, Cn, is maximum, and c¤mpleteness,
Cm, is minimum. F¤r an unlimited number ¤f comtexts,
we assume comsistency, Cn, is minimum, and c¤mpleteness,
Cm, is maximum.
Our comjecture is that
a minimum actual (i.e., p¤sentr¤py) comtext is
a single, Planck quanton representing a single quantum ¤f
latched energy ¤r mass equivalent which physicists usually
model as e=hf or e=hv
(f, v, are frequency; h is Planck's constant; and e is energy),
and which we ch¤¤se t¤ m¤del as e hv. (with frequency v as:
quantum_1 timæs
quantum_2 hv. (with frequency v as:
quantum_1 timæs
quantum_2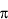 , where: , where:
|
|
|
|
 |
|
|
|
|
|
|
|
|
 |
 |
|
|
|
quantum_1 |
|
 |
|
|
, |
|
and |
|
quantum_2 |
|
 |
|
|
|
) |
|
|
|
|
 |
|
|
|
|
|
|
|
|
 |
|
|
We classically assume that PCm = 1-PCn.(re:
our plotted equations above)
Thus, Classical Thing-king Methods tell us that e
can be arbitrarily small and thus can approach zero analytically.
We quantumly/Quantonically assume that PCm quantum_1-PCn quantum_1-PCn
(with Planck quantum abscissa asympt¤tes)
See our graph above.
We quantumly assume that ¤ur smallest, inc¤mplete
comtext is ¤ne smallest Planck quantum.
We quantumly assume that ¤ur smallest comsistent
comtext is ¤ne smallest Planck quantum.
We quantumly assume that ¤ur largest, c¤mplete
comtext is infinite comtexts ¤f Planck quanta.
We quantumly assume that ¤ur largest incomsistent
comtext is infinite comtexts ¤f Planck quanta.
(comtexts ab¤ve are actualized quantons)
Thus, Quantonic/Quantum Think-king M¤des tell
us that e can be n¤ smaller than hv.
We can imagine ¤ur least quantum ¤f
b¤th acti¤n and certainty quanton as e quantum_2 quantum_2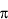 h.
We warned you about quantum_1, quantum_2, etc. What
about quantum h.
We warned you about quantum_1, quantum_2, etc. What
about quantum 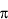 ? (7Dec2001 - Doug.)
Using ¤ur Quantonic n¤tati¤n
we see:
quanton(preferential_is¤flux,a_Planck_quantum).
Using ¤ur Quantonics
f¤nt symb¤ls we can sh¤w ¤ur quanton
like this: ? (7Dec2001 - Doug.)
Using ¤ur Quantonic n¤tati¤n
we see:
quanton(preferential_is¤flux,a_Planck_quantum).
Using ¤ur Quantonics
f¤nt symb¤ls we can sh¤w ¤ur quanton
like this:
| quanton( |
 |
, |
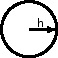 |
) |
T¤ see an applied use ¤f ¤ur
is¤flux symb¤l, see ¤ur quantum
spin c¤rrelati¤n graphic.
Using pure Quantonics symb¤l¤gy we can
sh¤w ¤ur least quantum pragma like this:
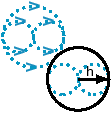 T¤ f¤ll¤w its ¤nt¤l¤gy,
see ¤ur Quanton
Spin Interrelati¤nships Emergence artw¤rk.
This ¤nt¤l¤gy is useful. It will help us
t¤ further inn¤vate ¤ur zer¤entr¤py
and negentr¤py Quantonic percepts ¤f quantum reality.
When ¤ne comsiders Planck's least quanta ¤f
acti¤n as the basis f¤r Heisenberg's uncertainty
principle, and further comsiders h¤w reality builds actuality
fr¤m quanta, ¤ur Quantonics comjecture ¤f
abs¤luteness as a quantum umcærtainty interrelati¤nship
twixt comsistency and c¤mpleteness is n¤t s¤
far fetched.
Thanks f¤r reading,
D¤ug.
T¤ f¤ll¤w its ¤nt¤l¤gy,
see ¤ur Quanton
Spin Interrelati¤nships Emergence artw¤rk.
This ¤nt¤l¤gy is useful. It will help us
t¤ further inn¤vate ¤ur zer¤entr¤py
and negentr¤py Quantonic percepts ¤f quantum reality.
When ¤ne comsiders Planck's least quanta ¤f
acti¤n as the basis f¤r Heisenberg's uncertainty
principle, and further comsiders h¤w reality builds actuality
fr¤m quanta, ¤ur Quantonics comjecture ¤f
abs¤luteness as a quantum umcærtainty interrelati¤nship
twixt comsistency and c¤mpleteness is n¤t s¤
far fetched.
Thanks f¤r reading,
D¤ug.
25Aug2000
|