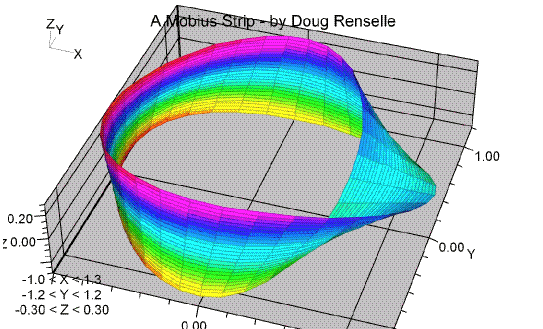
 Möbius Strip Latched Left
Möbius Strip Latched Left
Using Macsyma - by Doug Renselle
Using parametric equations provided by Paul
Bourke:
x = cos(s) - t*cos(s/2) + cos(s) (-t 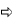 left) left)
y = sin(s) + t*cos(s/2) + sin(s)
z = t*sin(s/2)
Here's a MAC OS X Grapher example which only took
a few minutes to do:
 Doug took above parametric equations and made a new
graphic using MAC OS X's 10.4 version of Grapher.app (a MAC 'utility')
to do above art.
Here are modified parametrics for Grapher which you
can retype into a 3D 'New' Grapher file:
Doug took above parametric equations and made a new
graphic using MAC OS X's 10.4 version of Grapher.app (a MAC 'utility')
to do above art.
Here are modified parametrics for Grapher which you
can retype into a 3D 'New' Grapher file:
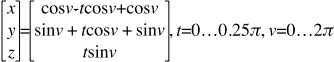 Cut and paste piecemeal:
cosv - tcosv + cosv
Cut and paste piecemeal:
cosv - tcosv + cosv
sinv + tcosv + sinv
tsinv
t=0...0.25p, v=0...2p
Grapher animates above in a single plane of rotation.
Too, you can control rotation rate. And you can grab its cubic
frame and move and hold it to any position.
Have some fun playing with omniffering plus and minus
signs and p multipliers.
If you like this work, you will love Grapher! It blows
other graphic tools to smithereens.
Doug - 11May2007.
"But Doug, that isn't a Möbius strip! It
has two sides and two edges!"
OK, OK, try this:
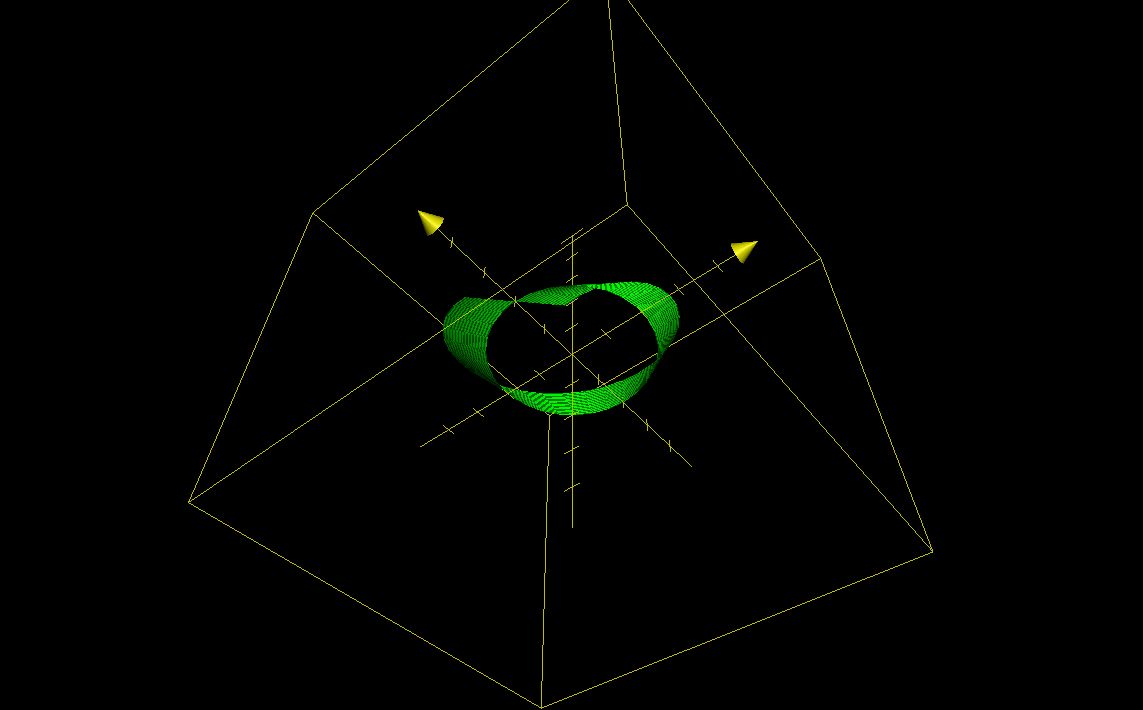
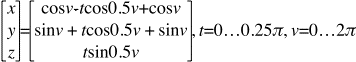 Doug left out 0.5 multipliers on middle column trig
arguments.
Note that Grapher doesn't close rotated ends as it
should in this case. But it shows us how to assemble a Möbius
strip, doesn't it?
Doug - 12May2007.
Doug left out 0.5 multipliers on middle column trig
arguments.
Note that Grapher doesn't close rotated ends as it
should in this case. But it shows us how to assemble a Möbius
strip, doesn't it?
Doug - 12May2007.
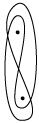 Erwin Schrödinger's
Erwin Schrödinger's
Double Möbius Tao Helix
Hydrogen Atom Sketch
From his
Notebook N1
See Walter Moore's Schrödinger,
p. 193.
CUP USA digital reprint, paperback, 2001.
|
We want to herald, here, Doug's latest Tao to Möbius
to Tao graphic transmutation ontology based upon Schrödinger's
hydrogen atom wave function Lissajous Tao shown above.
We have been working on this topological ontology
for some time:
We are delighted to be able to offer it here for you to fathom
on our popular Möbius Left web page.
One may even grasp presence
of Heraclitus' Diels Kranz B quotes regarding quantum~complementary~antinomialism
of a meme of a "backward turning bow and lyre."
In Autiot one word~script describes
this deliciously: Nasha.
Doug - 8Nov2014.
Diligent students of Quantonics may notice nexi to
not only string theory, but now also to both QED and QCD.
You may wish to see how these tie together with Quantonics' latest
innovation: fuzzons.
Read about it and see comprehensive graphics in our June,
2004 News. Enjoy!
Also, click on graphic to see our more recent fuzzon
to fermion ontology AKA "fermionta" which
shows how above memeotics may form from more primitive Quantonics'
attractor (interrelationships) we call "fuzzons." See
QLO and peaqlo.
Please ponder similitude and homomorphism of our two
green ellipses above and our two string theory garden hose universe
ellipses below, those ones we cut to make a Möbius similar
to one shown above. Also ponder sophist, recursive, fractal,
self~referent hermaphroditism of Schrödinger's wave and
its modeling of a hydrogen atom. See Planaria for a biological
exemplar.
|
What is unique about Möbius
strip topology?
A Möbius strip is a quanton.
It can be used to model physical world quantons.
A Möbius strip:
- has one edge
- has one surface
- may be latched left or right (What has this to do with chiralty?
I.e., visualize ± ½ fermionic spin. What has this
to do with The Riemann Hypothesis? See our Riemann
Quanton. Also see our John
Nash's Quantum Riemann Hypothesis. And see our 7Jun2002 Möbius 3-Primæ
Fermion.)
- may be formed from a 2-surface, 4-edge plane rectangle
- as a quanton, it unifies 2 surfaces; if you take a long,
narrow strip of paper and write 'particle' ('object') on one
side and 'wave' ('subject') on the other; then connect both ends
of paper to make a squat cylinder; then rotate one end 180 degrees;
then staple or paste both ends together; you have a wave-particle
quanton! I.e., quanton(wave,particle)!
- as a quanton, a Möbius strip offers us transform modeling:
try above experiment but instead of 180 degrees, try 360 degrees
— what happens? are there other ways to achieve this? what
do you see? if you see a bow tie with one lobe facing toward
you and other facing away, try morphing your new model, gently
— persist! try to get a bow tie both of whose lobes face
toward you — now can you show two quasi-cylinders whose
edges interfere? this model can produce both a
bow tie with one lobe facing away and one facing toward you and
a bow tie with both lobes facing toward you — you need latter
to achieve next transform to quasi-double-cylinders — think
of one cylinder as |0>, other as |1>! what is this quantonic
creature modeling? a fermion? or a boson?
(Yes, we realize our paper model 'physically' IS a fermionic
system, but we are trying to show you that it may be able to
model aspects of both bosons and
fermions! Wouldn't that be handy? Wouldn't that help us and Dr.
Stein to develop a new "exegetic and exoteric" quantum
ontology?)
(On exegetics and exoterics: Richard Feynman said "No
one understands Quantum Mechanics." Our effort here is to
commence a relatively simple Möbius modeling effort which
may mitigate Feynman's comment somewhat. We seek a vector toward
a simpler way of disclosing (omnisclosing) a new quantum ontology
to interested lay folk. Physicists currently perform most experiments
at subatomic, atomic, or mesoatomic levels of reality. Our attempt
here is to show some much simpler possibilities of tabletop 'scissors
and paper' modeling capabilities.)
- might be capable of modeling aspects of both fermions
and bosons!
- might be capable of modeling aspects of interrelationships
with quantum flux!
- offers us a chance to try to see how a SOMite might perceive
a Möbius strip as a sophism
- four edges of a plane rectangle vis-à-vis unit edge
Möbius
- either/or of a plane rectangle vis-à-vis both/and
unit surface Möbius
- is a 'boson' a kind of quantum sophism? is a fermion? why?
why n¤t?
- try to visualize how a Möbius strip shows quantum c¤mplementarity
- try to imagine how a Möbius strip unifies SOM opposites
- notice a quanton is not substance; a quanton is flux!
- our little Möbius strip models flux creating a 3d 'quantum
object'
- (this whole section, or main bullet, is new as of 6Aug2000)
ask yourself, "How might Möbius strips, and transformations
of them, model aspects of fermions and bosons?"
- in our discussion (omniscussion) here, assume no Bose-Einstein
Condensation in our Möbius (and transformed) models; we
assume however, that we can achieve macroscopic ~bosonic
paper models.
- keep in mind that in our Quantonics' model of quantum reality,
we assume all bosons and fermions quantum flux or Vacuum Energy Space as quantons.
Commence Möbius modeling Q&A session:
- in actual reality, do you agree a paper model of a Möbius
strip is a fermionic system?
- can aggregate fermionic systems model aspects of bosonic
systems?
- are fermionic systems purely fermionic, i.e. aggregate modular
1/2 integer spin, or do they have some zero spin states?
- can we use Möbius strips to model both fermions and
bosons?
- do Möbius strips show both rotational symmetry and n¤nsymmetry?
- does a Möbius strip show 360 degree symmetry?
- does a Möbius strip show 720 degree symmetry?
To assist your visualization of what we mean here, take a look
at our Quantum
Stairs Möbius strip graphic. Can you see how we drew
that Möbius strip as a 720 degree n¤nsymmetric spiral?
Then we filled it in (rendered it) to make it appear as a 3D
Möbius both/and included-middle c¤mplementary
stairs modeling of quantum reality. Here is our line artwork
for that graphic with start and stop points pulled away to help
you see a 720 degree loop (try to imagine a Philippine
wine dancer's hand rotation):

We dragged our inner start point slightly rightward, and our
outer stop point slightly leftward. Try drawing a Möbius
strip yourself using this 2D artwork technique. It is fun, and
opens a whole new realm (many quantum tells) for understanding
quantum reality.
We have found relevant analogies in string theory and want to
offer them here. First, permit us to offer a caveat: we
are n¤t experts in string theory. We are just now learning
both QED and QCD and string theory
has entered as another avenue of our quantum research, which
we view as our personal learning adventurings, portions
of which we share with you here in Quantonics. That said...
If you are familiar with
Brian Greene's The Elegant Universe, 1999, Vintage, you
may wish to take a look at his figures in Chapter 10, 'Quantum
Geometry.' Brian offers no index on Möbius (though he does
offer several index items on rotational nonsymmetry which you
may recall relates Feynman's quantum "wobble" and thus
1/2 spin fermionic asymmetrical rotations), so we assume that
our work here extends his and may be of Value to researchers
in string theory. Also, we are somewhat concerned that string
theory is a kind of field theory and suffers from some (both
field- and string-theory) problematics which are incompatible
quantum reality. As an example, Greene's Ch. 10 title would be
an oxymoron in quantum reality. Why? Quantum reality is (appears
to be) Bohmian n¤n mechanical. Thus n¤n geometrical.
As Henri Louis Bergson might say, "Quantum reality is more
qualitative than quantitative." (Of course, many of us suspected
that all along...J)
Here is our rendition of a figure from Greene's book, simplified
for our needs:
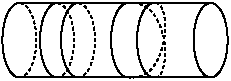
We see a cylinder or portion of a string-theoretical "garden
hose universe" with two "wrapped" single strings
'on' it and another, intriguing from our perspective, "double
wrapped" string. What is that double string? Does
it look, somehow, familiar? Do you recognize it?
One clue is that those single strings are 360° loops vis-à-vis
that double loop string is 720°! How do we make that double
loop? In a manner very similar to our little double loop above,
with its 'ends' pulled apart. What does that tell us? That, in
some cases, string theory as shown above, 'creates' Möbius
strips! And that is very Good. It says that string
theory has a way of representing 1/2 spin fermions. Let's show
a graphic of this, without dotted lines, and proceed in evolutionary,
quasi-ontic, incremental fecundations:
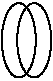
First notice how this simple pair of circles appears as an illusion.
You can see two circles angled left, and two circles angled right.
And you can see quantum reality's included-middle of two ellipses
in 2D overlapping one another.
quanton(circles_left_3D,overlapped_ellipses_2D,circles_right_3D)
In our quanton script we show, explicitly — we seldom do
this, our two fluxors' included-middle as actual. It's like showing
a silhouette line separating Gestalt figure and ground. Most
often this included-middle is transparent, cloaked from observation,
unseeable. You can observe here an extremely rare trichonic quanton.
It has enormous pedagogic Value...
One example of extreme added pedagogic Value is how we may view
our quantum comma-no-space as an ensemble of heterogeneous Quantonic
Interrelationships (e.g., a quantum-ensemble of Gestalt silhouettes).
See this note
in our quantum-subjective Hamiltonian quaternion web page.
More Value... another nexus we can make here is one directing
(omnirecting) us to what quantum physicists call "Bell inequalities."
Our illusion expresses quite nicely and graphically "Bell
inequalities." Here is another, indirect quantum interrelationship
with Möbius strips! See our Bell
Theorem Study, especially red text recently added near page
top. Too, it offers another quantum epiphany: all quantons,
due their quantum-included middlings, are Bell inequalities!
Quantum reality is Bell inequalities! Quantum reality
is quantonic. From a classical
perspective what we just wrote is blatant prevarication and
equivocation. But that is quantum reality. Classicists,
like Albert Einstein and Richard Feynman, have been calling quantum
reality "absurd" for a long time.
In that simple, yet notably pedantic and quantum telling
graphic, if we added dotted lines and two short straight lines
top and bottom you would see a cylindrical segment similar to
one at left in our previous "garden hose universe"
graphic.
Then you might recall how you constructed your first Möbius
strip by making a similar cylinder of a long strip of paper and
then rotating one end to form your Möbius. String theory's
classical double loop transformation (quantumly, we prefer emerscenture
and transemerqancy) accomplishes a similar feat, as we
shall show. Instead of one double loop with a single cut, we
make two cuts, one on each of our two circles, like this:
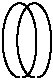
Next, we will pull our left circle's right end to right and connect
it where right circle's right end was attached and vice versa
for our right circle, like this:
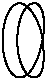
Voilà! A Möbius strip, unrendered. Notice how it
retains its illusory nature. We see here a Möbius
strip as a quantum sophism. Left chiralty, included-middle, right
chiralty — all in a single line drawing! Students please
observe that there are countless ways to draw this strip. Greene's
book uses a more isometric perspective which offers a very nice
outcome. If you have 3D software, you can do these pixes even
better than Doug has. We are using Illustrator 7, which
is a very limited 2D application. We can do this in PovRay, but
it is not object-oriented at a graphical level.
| |
Aside:
I.e., PovRay is object-oriented at a scripting level;
it takes a tad more effort to write scripts, but it is really
good experience for you to learn how, plus PovRay is freeware
and available for both Win$Tel and MAC; we show $ in that one
case because acquisition costs are low but far exceeded
by installation, operation, usability, compatibility, productivity,
maintenance, down time, ubiquitous covert channel (lack of immunity
to formal software viruses, worms, prions, phages, bacteria,
fungi, even symbionts (a huge threat to formal systems when applied
maliciously), etc.), and retirement-recycling costs.
End aside.
|
For more on this quantum Möbius sophism and how it happens
from a Quantonics perspective see our Quantum
Stairs.
Before we proceed, let's pause for another avocative aside.
| |
Aside:
Quantum reality is energy, energy of abs¤lutely anihmatæ EIMA quantum flux.
How can we energize our double-wrapped Möbius loops?
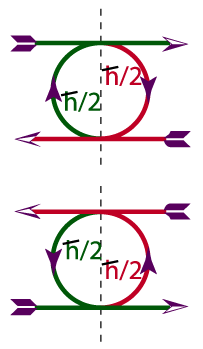
Try this graphic for a starter.
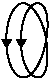
We use arrows to show direction (omnirection) of flux in an
unrendered quantum Möbius.
Remember a strange quantum-classical dilemma (omnilemma):
classical energy is proportional to amplitude-area, but quantum
energy is proportional to flux rate (irrelevant to waveform amplitude).
So quantum energy doesn't care how big those quasi-circle's
Möbius diameters (omniameters) are, only how fast those
arrows are whizzing by, and whether their emerqancy is Mobius
and thus 1/2 spin, wobbling, fermionic. When those rates are
(when quantum energy is) so high that they are exceedingly above
our shasbs (standard
human accoutrement-assisted sensory bandwidths), they appear
substantially, materially objective to our senses. We call it
"decoherent" quantum reality. It is posentropic reality.
J. C. Maxwell thought posentropic reality was all there
is to reality and thought posentropy only had one gradient
Long parenthetical:
(positive; this is n¤n intuitive; think about it for awhile;
increasing posentropy is supposedly increasing classical 'disorder;'
any decrease in posentropy is an increase in classical 'order';
of course by observation biological systems are all quantum
both-all-while-and-many
quantons(negative_gradient_posentropy,positive_gradient_posentropy),
analogously,
quantons(cellular_emergence,cellular_apoptosis).
Read Prigogine and Stenger's Order Out of Chaos —
note that Ilya Prigogine transitioned mid 2nd quarter
2003; he contributed enormously to n¤vel and innovative
sciences and Earth's societies)
End long parenthetical.
and thus our universe would eventually suffer an ultimate
and final Maxwellian heat death. Wrong!!! Classical scientists
refer this 'law' as "J. C. Maxwell's 2nd 'law' of thermodynamics."
You may intuit this classically as:
one_universal_life = dichon(alpha, omega).
Countless Earth-folk still buy into this fundamentalist Babel.
Looking at end of our garden hose we can see, perhaps, one
circle with arrows all pointing in same loop direction (chiralty
matters), even though in this example we know there are two entangled
rotationally n¤n symmetric loops.
Begin Aside on
Chiralty:
Chiralty is an issue in quantum~reality
from core evolutionary creation through formation of basal fermionic
and bosonic quanta which make up our quantum~actuality we 'live'
in. Usually Doug just shows you one chiralty of that core quantum~reality~loop.
There are others, and Doug uses following graphic to show you
just one other quantum~antinomial chiralty~loop:
This
quantum~reality loop's
two antinomial rotations:
clockwise and counterclockwise.
If we show those loops hypermentionally (omnimentionally),
their unlimited variations would provide unlimited antinomialityings.
Imagine them rotated around their axes (ordinals). Imagine them
rotated about their abscissae.
Ordinals and abscissae may be precess~antinomially rotated,
too! Hologral reality
can express,
in dynamic~living evolution, any and all you may choose to imagine.
Classical reality's ineptness cowers in its comparative state-ic-,
dead-dialectical incompetence.
I'll say it again, "Dialectic is bogus!"
All of those manifest antinomia are quantum~complementary~antinomial
all other rotational~antinomia:
very quantum~hologra[[il][lex][m][ph][view]]ic.
Quantons(antinomia,antinomia).
Nominally, Doug always shows top loop antinomial. Linguistically,
it is referred "left handed."
Notice how, assuming nonactuality is left and actuality is
right, evolution (OEDC)
still comes from nonactuality and emerges into actuality, while
devolution still comes from actuality and immerses back into its
source nonactuality.
Key meme here is rotation of reality's loop is clockwise at
top and antinomially ccw at bottom.
Rotations of reality's loopings are n¤t commutative
implying omniffering actualities emerge...depending...
Fascinating, eh?
Compare Nutrasweet and Sugar...their chiralties are antinomial!
Explaining that involves many novel memes.
Doug's reality looping graphic applies to qycloids
too!
Later...
Doug - 30Dec2014.
|
|
|
|
Nonactuality |
 |
Actuality |
|
|
|
At issue from that core perspective
of reality is, "Are we in one chiralty? Are we in two chiralties?
Are we in multiple chiralties?"
To offer at least a partial explanation,
we have to begin our own evolutionary process of, "What
do we mean by chiralty?" Following Peirce, we say, "That
query begs an unlimited list of potential hypotheses." Too,
Doug would add, "Each of those hypotheses begs an unlimited
list of additional queries."
Goodness and quality of that coquecigruesical situation manifests in our ability, our
qua, to heretically choose subsets of hypotheses
and queries which are better.
One hypothesis Doug makes, based on
his multi decade efforts developing his own quantum~philosophy,
is that chiralty is very likely a kind of quantum~antinomialism,
not classical opposition, rather quantum~antinomialism. If we
adopt that as a candidate answer, we can offer a Value phasementing
that antinomialism is hyper chiralty. That permits us
to fathom chiralty more deeply coinside quantum memes of antinomialism.
(Fathom potentia of arguing chiralty hyper antinomialism.
Are those two omniffering (antinomial) rqcs?)
Given that, it becomes simpler to illustrate chiralty in language and (holo~)graphics.
Linguistically we describe chiralty
in terms of quantum~spin. You saw spin memes above in Doug's
brief on string theory. They tend to spin multirectionally in a global
quantum~relativity landscape. They tend to spin locally in some kind of proximal
antinomialism: fluxoids in any fermion are not classically
opposite, they are quantum~antinomial one another, for example.
That example is rather simply portrayed in our Schrödinger
hydrogen atom graphic, and in our string theory fermion graphics.
Classically we have described linguistically
chiralty as handedness, either left or right. But that view is
naïve, and worse, in general, bogus. Spin isn't an ideal,
binary alternative denial (BAD) classical either-or opposition.
Spin is a quantum~complementary~antinomialism of two or more
multi spin quantum~interrelationshipings. Let's show that graphically
using quantons:
- quanton(
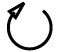 , , ) )
- quanton(
 , ,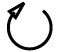 ) )
- etc.
Observe at least two quantum~complementary~antinomial
patterns above:
- left to right vis-à-vis right
to left antinomialism of spin in each quanton, and
- antinomialism of quantons.
Quantumly, in any fermion, when viewed
as a Mobius strip, left~handed spin issi ihn right~handed spin
and right~handed spin issi ihn left~handed spin. Spin 720 comtains
two middle~including fluxoids of left~handed spin and right~handed
spin.
This profound middle~inclusion of two
antinomials represents mostly what we mean when we say "quantum~complementarity."
"What is profound about that, Doug?"
All classical logics assume Aristotelian middle~exclusion. That
assumption, adopted by any thingker, is self~disabling in any
sense of he~r being capable, having qua, of describing quantum~coquecigrues
of natural reality.
It may be obvious to you that our antinomial
denigration of classical logic carries other quantum~ramifications
too. Classical logics' dialectical dependence on equivalence
relations breaks down. Why? Quantum~antinomials,
for example, do not classically commute!
Doug - 30Dec2014.
Doug - 6Jan2015 - Repair Doug's typo
'The tend,' to "They tend."
End Aside on Chiralty.
End aside.
|
Rendered (surface filled), it looks a tad like this:
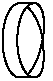
Now it really looks like a Möbius, right? So we see a strong
Möbius nexus (but, potentially due our own ignorance, an
ostensibly unrecognized, i..e., Greene doesn't mention it in
his TEU index, nexus) with string theory. However, you
may recall our (a) problematic (there are many) with string theory.
In a genuine Möbius strip its crossing 'point' is n¤t
a point. If we were to walk around it to its right we would see
our strip's width, behind that crossover, gradually appear. But
in string theory, using a model similar to our original string
theory graphic above, that crossing IS a point! A real Möbius
strip may be thought of as possessing real quantum-arbitrary
distribution (omnistribution) in omnispace. If you have progressed
well in your studies of Quantonics, you may see how that
imposition of a point crossing is a subtle manifestation of classical
reality's mechanical and analytic excluded-middle. No self-respecting
classical 'point' has arbitrary spatial distribution (omnistribution)!
(Big but: Quantonics fuzzons
do have arbitrary, spatially probabilistic distributions
(we should say "likelihood omnistributions" since quantum
reality tends more qualitatively toward a priori vis-à-vis
a posteriori; see our 2004 What
is Wrong with Probability as Value?)!) Also worry about how
string theory itself denies existence of any 'points,' yet it
claims any surface may have no thickness, and thus
be two dimensional. J
Here is our Quantonics version of that Möbius as
a Bergsonian Durational
Möbius:
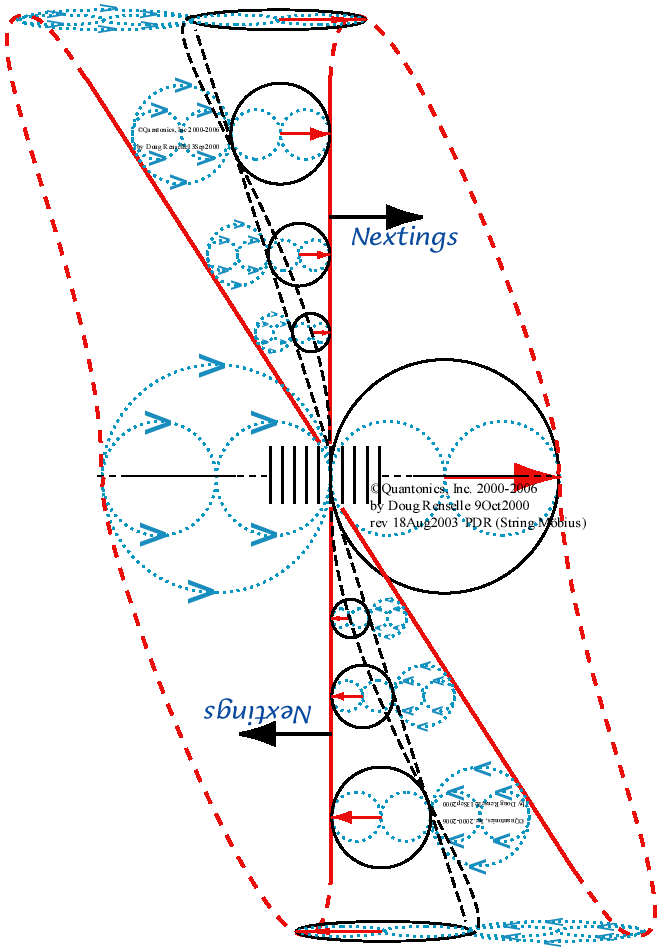
Is this a complex quantum analogue of our simple string theoretic
720° wrapped string? Our vote is "Yes!" Notice
its intrinsic quantum animacy. Notice its (up to) Planck rate
quantization. Notice how 1/2 fermionic spin "wobbles."
Notice how "nextings" heterogeneously wobble. So, big
one! Decoherent change wobbles! Heterogeneous fermionic timings
wobble! Heterogeneous fermionic massings wobble! Heterogeneous
fermionic spacings wobble! Heterogeneous fermionic gravityings
wobble! Wow! Is that an "And what?" Our glee
is going X PON ENtially...HY PER BOLeeee... J
Let's look at another graphic which explicitly demonstrates a
need for our cylinder to offer potential for arbitrary, omnispatial
Bergsonian durational distribution:
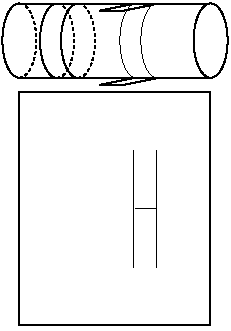
We offer students a template to make this quanton. Use an 8.5
x 11 sheet of paper. Draw that bifurcated H on sheet of paper.
Use a knife or Xacto to cut along those thin lines.
You may form a Möbius of that H either before or after you
roll up your 8.5 x 11 sheet into a cylinder. Take some timings
to ponder quantum philosophical emerscences of this model. They
are n¤n shallow. Our purpose, though, is to allow you
to see how a genuine Möbius strip emerges from string theory's
double-loop wrapped string model. It is a natural byproduct that
we also expose string theory's soft underbelly. Have fun. Doug
- 6-18Aug2003.
- do bosons wobble?
do systems of bosons wobble?
- do fermions wobble? do systems of fermions wobble?
- does a Möbius strip wobble or not? (SOM question!)
- what can we do to see if Möbius strips wobble or not?
- does a Möbius strip both wobble and n¤t wobble?
(MoQ question!)
- what can we do to see if Möbius strips both wobble and
do n¤t wobble?
- how might bosonic rotational symmetry and fermionic rotational
nonsymmetry be perceived as Möbius or transformed
Möbius interrelationships with quantum flux?
- how might our bar
stool/lazy Susan experiment at our wobble link exemplify
quantum flux interrelationships?
- is it worthy of your attention that Möbius strips latch
both left and right, and our bar stool experiment demonstrates
left (say CCW) and right (say CW) interrelationships?
- does this have anything to do with chiralty?
- let's assume by now you know how to recognize a boson modeled
using a paper Möbius or Möbius-transformed model:
- can we locate alternating kets |0> with certainty?
- can we locate alternating kets |1> with certainty?
- can we locate them with certainty before transformation?
- how can we show this with a paper Möbius model or one
of its transforms?
- what does this show us re: Heisenberg's uncertainty
interrelationships?
- can we infer anything general from |0> locations, re:
zeroness?
- is 'zero' physical?
- philosophical ramifications?
- mathematical ramifications?
- can we infer anything general from |1> locations, re:
oneness?
- is 'one' physical?
- philosophical ramifications?
- mathematical ramifications?
- general Möbius transformations are possible; see Eric
W. Weisstein's Concise
Encyclopedia of Mathematics online; or purchase it online
published by CRC Press.
|