|
|
Michael Talbot in his, The Holographic Universe, tells us how David Bohm sees this situation, "Bohm rejects the idea that particles don't exist until they are observed...He simply feels that most physicists go about it the wrong way, by once again trying to fragment reality and saying that one separate [classically objective, dialectical, analytic] thing, consciousness, interacts with another separate thing, a [classically objective, dialectical, analytic] subatomic particle." See p. 49 of 338 total pages of Talbot's THU. (Our brackets.) Doug - 2Aug2004. |
|
"The real difficulty lies in the fact that physics is a kind of metaphysics; physics describes "reality." But we do not know what "reality" is; we know it only by means of the physical description!" —Einstein to Schrödinger, 19 June 1935 |
|
Aside: Our last sentence above, feels like a downer. For classical science, it is. However, for quantum science, it is an upper! Classical invariance and its accoutrements like state, immutability, 1-1 correspondence, cause-effect, induction, and so on... are necessary for classical science's 'existence.' Without those accoutrements classical science disintegrates, massively. That sounds as though all is lost. Not to fear dear readers. Giving up those naïve and silly classical notions offers potential for immense gains. Quantum gains. Classical science insists that it must control Nature using dialectic and formal mechanism. That apparent control has allowed humankind a great deal of apparent progress during its last two millennia. So, again apparently, to give up classical science feels as though we have to give up all that progress. That is n¤t what we are saying or offering! What we are saying is that instead of attempting to control Nature (a futile effort), rather we assume a quantum posture and assist Nature. Become Nature's agents and partners in progress. Why? Nature will never allow us to control He-r! But what does Nature give us which is even more powerful than any modicum of control over He-r we might seek classically? Nature gives us free will and choice qualified by He-r mandate that we and S-he are an ensemble, actually, quantum ensehmblings. Our free will and choosings affect and are affected by He-r own free will and choosings. N¤ ch¤¤sings of ours are ever uniquely our ch¤¤sings. Our ch¤¤sings can never be objectively independent of He-r choosings and vice versa. This is what Pirsig and Herrigel mean by "we are in He-r and S-he is in us." (Paraphrased.) That is what we in Quantonics semantically intend by "Nature's n¤n-Aristotelian everywhere-ass¤ciative ihncluded-middlings." AH has told us that he has a friend who says that evil can never win in any long term. Why? How? Evil has two enemies: itself and Good. Good only has one enemy: evil. We like that parable. Let's use something similar in our discussion here. Humankind (to be general, less anthropocentric: sentients, e.g., Betelgeuseans, Capellans, etc.) can never completely win without Nature assisting their teams. Classical science believes we can win by controlling Nature. Classical science has two enemies: itself and Nature. Quantonics' version of quantum science believes we can only win with Nature's help. We must become quantum agents of Nature. We must be in Nature and assist Nature in He-r being co-inside us. Another way of saying that in quantum comtext of this web page: "We must, sustain, and nurture unlimited Bell inequalities co-with-in Nature and us." Every Value/Quality we have, every Good interrelationship we have is a Natural Bell inequality. Why is It (i.e., any Quality interrelationship, any quanton) an apparent classical inequality? Both Nature and we are in It and quantum ensehmble coobsfecting It. To classicists, It looks like an 'inequality.' Classicists wear blinders, therefore they 'cannot' be in any quantum pr¤cessings of k-now-ing "the rest of the story." Doug - 4Aug2003. End aside. |
|
It is our view that Quantonics offers superior ways of thinking about and interpreting reality. Quantonics achieves higher plateaux of thought several ways, chiefly using Robert M. Pirsig's Metaphysics of Quality (MoQ), and quantum science. We think Bell's Theorem offers us an opportunity to show you that superiority, and this document offers you a taste of it. What we will do here is use text from a Bell's Theorem decision tree in Gary Zukav's superb book, Dancing Wu Li Masters. First we will show his decision tree as tabular text similar to Gary's original portrayal of it. He portrayed Bell's Theorem classically, but he did not show SOM's either/or dichotomies separated and enclosed by SOM's schismatic wall. As you will see below, we use a triple-line border to illustrate SOM's wall. Then we will migrate to a more Quantonic view using Quantonic language for classical dyads that we call "dichons," and Pirsig calls logically positive bivalent "platypi." Dichons statically model ideal classical, objective, closed, propertyesque dyadic interactions. Finally we will migrate that emphasized classical view to a mixture of labeled 'classical' dyads and Quantonic omniads mixed together as quantons. Let's look at some examples which will introduce and perhaps help clarify our intent:
As we hopefully clarified in our list above, quantons dynamically model real c¤mplementary quantum interrelationships when their parameters are Quantonic (i.e., omniadic fluxors). When their parameters are static (i.e. state-ic), like SOM's dyads, our quantons only depict, for our limited local purposes here, static SOM things framed in a Quantonic comtext. We shall use three out of four of these examples in our Bell's Theorem study below. (We choose n¤t to use a Bohrian "exclusive" complementarity example below in our Bell's Theorem study. Why? We have Bohr's prolific works to show his intentions and classical "(un-)ambiguities." Doug - 16Jan2002.) Our sequence of transitions will take you only part way to a full Quantonic picture of quantum reality, but you will see our Chautauqua evolve from classical paradice into one unique perspective of quantum reality. We will build our first table derived from Gary Zukav's flow chart on page 317 of his Dancing Wu Li Masters (paperback, 350 page edition): |
||||||||||
 |
||||||||||
|
Legend 1 -
|
||||||||||
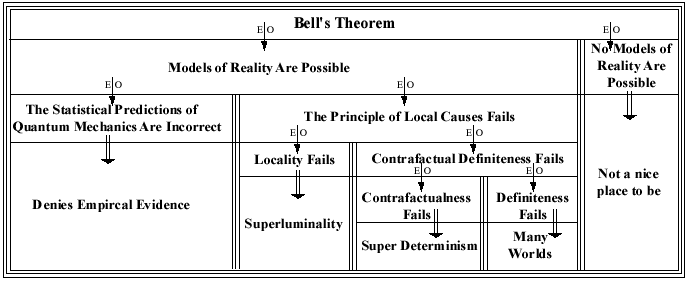 Figure 1 - Classical Bell's Theorem Originally Depicted by Gary Zukav as a Decision Tree |
||||||||||
|
We want to re-interpret this table using our Quantonic Think-king Modes. However, before we do, we want to review some SOM vis-à-vis MoQ fundamentals. Looking at our SOM tabular version of Bell's Theorem above, in Figure 1, what do we see? We see SOM's closed, dichotomous, either/or,
objective approach to analyzing reality.
Those two bullets exemplify perfectly what we mean in Quantonics when we say "SOM uses Classical Thing-king Methods, or CTMs." Each statement is a formal monad. SOM's wall denies any complementarity or c¤mplementarity twixt these two dyadically either/or related monads. So we may conclude, when we use CTMs that decision row one in our table above is an either/or represents SOM's excluded-middle Aristotelian wall.) Quantum science and our Quantonic interpretation
of it say it is better if we use Quantonic Think-king Modes (QTMs)
to study Bell's Theorem.
Both of these statements are quantum c¤mplements (Mu's) of one another.
But what about that classical 'not'
Doug? Good question. Classically 'not' is formally and radically
mechanistic. A classical 'not' implies formal classical negation.
However, Henri Louis Bergson, et al., show that classical negation
is not real when interpreted as formal negation. They show that
negation
is subjective. Some of them did 'not'
realize it, but they show that, in a quantum or Quantonic comtext,
'not' is a quantum c¤mplementary term. Our coined version
of a quantum c¤mplementary 'not' is 'n¤t.' Also see our n¤vel Quantonics'
English Language Remediation of n¤t Their uses of CTMs also force them to view singular static models as implicitly inanimate except for analytic uni-temporal objective motion, e.g. classical object y=f(t). CTMs permit orthodox practitioners (an axiomatically assumed convenience) to uni-temporally stop classical reality and thus allow objective state-ic observation of any classically contrived model. Also note, in decision row two, in their
classical view of Bell's theorem how their classical analyticity
forces them to assume classical causation. Consider that they did not even question whether
causation is problematic in their 'analyses.' They assumed one
cause and one effect. Outcome: Only one
possible static model of reality! CTMs deny both quantum pluralism
and quantum Dynamic Quality's existence, again, axiomatically.
Their works have ingrained much classical unilogical Boole!
This terminology, viewed classically,
is a source of grief for classicists who use CTMs to attempt
any understanding of reality.
Those of you who are students of Quantonics may see now how comtrafactualness uncloaks quantum reality's many islands of truth. Many quantum comtexts. Many truths! This is precisely how quantum reality rebuffs classical axioms of independence, localability, isolability, separability, reducibility, commutativity, distributivity, factorability, etc. This is why we say, "CTMs are naïve." This is why we say QTMs are better, especially if you want to do more realistic modeling of reality. Very briefly let's comsider some differences twixt a homological monistic classical 'model' of reality and many pluralistic quantum models of reality:
By comparison to SOM's dichon, now, we see a MoQ/Quantonic quantum included-middle n¤n-Aristotelian interrelationships.) and we must assume our modeling is quantumly both dynamic
and static, i.e., quanton(dynamic_flux,static_flux). From this
we may see how Pirsig's MoQ showed us that reality models itself
as quanton(DQ,SQ). We can show — that fundamental quanton(dynamic,static)
— applies to all quantum reality. All quantons of reality
are both dynamic and static, and they share c¤mplementary,
c¤mpenetrating interrelationships — Quantonic interrelationships.
(Note: Pirsig's SQ is n¤t classically static. It
is quantum static. Quantum static flux is actualized (via quantum
measurement) from nonactualized quantum dynamic flux. Quantum
static flux is always emerging, mutating, or demerging under
impetus from quantum dynamic flux. Pirsig's DQ is quantum reality's
absolute changæ
impetus. SQ is DQ's actualized agent of pluralistic evolute changæ. For a superb example of
"persistent, inertial quantum 'static/latched/fretted/measured/decoherent'
flux," see our qubit example near page top. This is a most
difficult aspect of quantum reality to describe. Why? As yet,
we have n¤ memes for Feynmanesque "understanding"
how it happens. Closest we can offer is our heuristic, graphical
quantum actualization
ontology. Now, in 2004, we can offer more heuristics. See
our 2004 fermionta
and our 2004 Generation III Quantum
Reality Loop. Doug - 7Nov2004.)
QTMs assume reality is animate, and that DQ is real and exists,
and further that DQ is SQ's quantum c¤mplement. SOMwits
who practice CTMs deny such a statement as, "ridiculous
and absurd." |
||||||||||
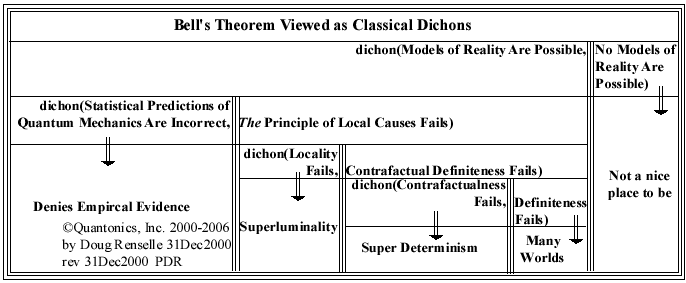 Figure 2 - Classical Bell's Theorem Depicted Using Quantonics' Dichons and SOM's Wall |
||||||||||
|
Consider any subjective nature of "No Reality Models
Possible" based on our comments above regarding classical
interpretations of 'not.' And remember how classicists consider
such a statement 'absolute.' Did you get that? Classicists 'conceive'
no and not as formal logical 'absolutes.' Yet they
derived their formal predicate logic from an Aristotelian, physical,
material substance foundation! And their logic is inutile
dealing with quantum physical reality! There are few better ways to antagonize classicists than to
show them their uses of 'not' and 'no' are subjectives. Have
fun! In our table just above we retain all
of Zukav's original statements; however, we show them as classical
legacy either/or dichons. |
||||||||||
 |
||||||||||
|
Legend 2 -
|
||||||||||
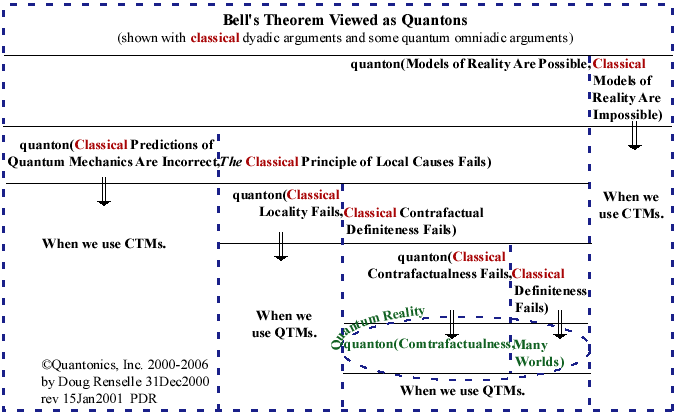 Figure 3a - Classical Bell's Theorem Depicted Using Quantonics' Quantons and MoQ's Face of Changæ |
||||||||||
|
Reader, pay particular attention to our ellipse above in Figure 3a, labeled 'Quantum Reality.' It 'encapsulates' some essence of quantum reality. Greatest value of Figure 3a is that it shows beautifully how inept CTMs are at using formal 'logic' to understand reality. Without QTMs, we would n¤t be able to show you this blatant SOM ineptness. It also shows that 'failure' is not failure, rather it offers success if one is willing to changæ one's ways of thinking. Figure 3b is a simple extension of 3a showing an extended portion of quantum reality which includes superluminality as did Gary Zukav's original decision tree: |
||||||||||
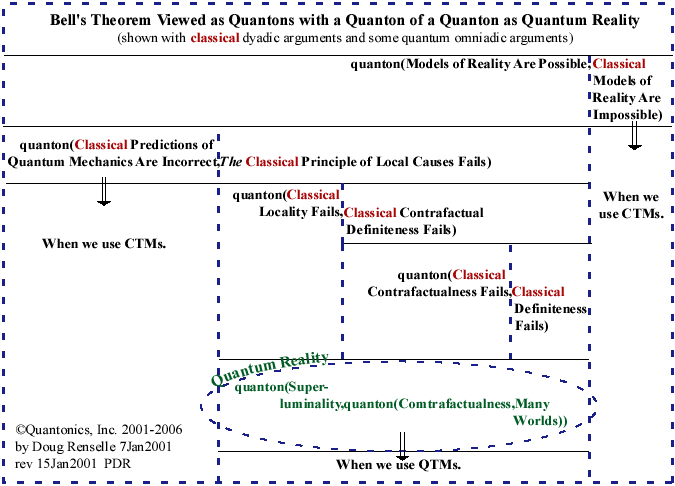 Focus
on QR Ellipse. Focus
on QR Ellipse.Figure 3b - Classical Bell's Theorem - Figure 3a Extended Showing Quantum Reality as a Quanton of a Quanton |
||||||||||
|
Figure 3b shows us that quantum reality's classically perceived dichonic absurdities ("failures") — when viewed with Quantonic optics — become quantum included-middle both-all/while/and-many "inclusive-" c¤mplementary opportunities. Gary Zukav's classical decision tree method is innately (by classical design) incapable of showing our real quantum outcomes. Please remember that our quantons represent:
For Millennium III make a millennial resolution to gradually unlearn CTMs and replace their naïveté with QTMs. Evolve yourself from SOM thing-king toward MoQ think-king! |
||||||||||
| 1Jan2001 Doug. | ||||||||||