|
Probability - a posteriori
(see a priori, below under Likelihood)
Margenau shows us unambiguously that probability is about
ensembles. Classically, any ensembles must be ensembles of ideally
homogeneous and state-ic actuality3.
Certainly then, classicists resist any notions of ensemble probability.
It, quite simply, denies any classical notions of absolute determinism.
Margenau offers a simple yet crucial observation: "Probability
is not about single events." We can make an inference here,
"Single events are improbable."4
Stronger: "We cannot predict single event probabilities."
(Note a fine point that "single events" only occur
once; they are quantum novel.) However we can predict
probabilities of events which appear to recur. Why do
we say, "...appear to recur?" In quantum reality
classically ideal ensemble recurrence is simply impossible. Classicists
ineptly force an appearance of ensemble recurrence using stoppable
reference frames and 'reproducible,' 'identical,' 'conventional-conveniently-Flatland-limited,'
'initial conditions.' These are just more classical delusions
(even when viewed macroscopically and cosmically). Reality is
not stoppable! However, reality is quantum sophist! Quantum reality
is fractal~sorso.
So Quantonics can extend Margenau's observation. "Probability
is not about novel events." Probability demands heterogeneity!
Probability has no meaning in an entirely homogeneous, i.e.,
classical, system.
Latter blends a quantum hue into chance: affective
local and nonlocal ensemble choosings.
Classical chance is about actuality (its 'known' constituents)
and offers no capability of assessing any novel emergent events.
Notice how this nicely explains why classicists have been unable
to describe interstate process. Interstate processes always
harbor some quantum novelty! We call it "quantum chaos."
Yes! You are correct, to retain our quantum chastity we must
say, Bergsonian durationally,
"There is no (ideal classical) state."
Quantum chance shows us that novel realities may emerge which
we have not seen before, which have had no prior existence. First
'time' this happens, it is apparitionally, only apparently a
classical, single 'event' and classical probability has no means
of anticipating it. Students of Quantonics, however, are vividly
aware of quantum times as heterogeneous. So in quantum reality,
apparent classical single events, are rather, animate EIMA quantum
ensembles. We call them "peaqlos." See our discussion
of peaqlo at our
3D Fuzz¤n.
This added text is relevant our page top box, re: "nowings."
Nowings imply heterogeneous ensemble timings.
So what do we intend when we say, "heterogeneous ensemble
timings?"
In Quantonics we intend "all hermeneutics and perspectives
which are quantum affectings nowings and nowings' CH3ings."
So, then, what are those? Are (none, some, any, most, all) ensemble
pastings' ensembles affectings nowings? Yes. Are (none, some,
any, most, all) ensemble nowings' ensembles affectings nowings?
Yes. Are (none, some, any, most, all) ensemble futurings' ensemble
potentia affectings nowings? Yes. Again, we see an extraordinary
and unusual trichotomous quanton(pastings,nowings,futurings)
which is a more fuzzonic quantum animate, heterogeneous,
EIMA analogue of classical reality's unitemporal
time line and Einstein-Minkowski's
space-time light cone.
"But Doug, how can ?" Via memeos of quantum expectation, quantum anticipation,
quantum a priori. Margenau calls it "likelihood."
We quantumly think of quantum reality as capable of qubital
(Bohm might say, "holographic") computation. If that
is so, then quantum reality "quantum computes" all
potentia, all likelihoods. Quantum reality anticipates all potentia
more and less. Now some essence. Doesn't this show explicitly
"why ('classical') quantum theory ('mechanics') quasi~works?"
We say, "Yes!" Doug - 14Aug2004.
|
Probability - a posteriori (see
a priori, below under Likelihood)
Margenau shows us unambiguously that probability is about
ensembles. Classically, any ensembles must be ensembles of ideally
homogeneous and state-ic actuality3.
Certainly then, classicists resist any notions of ensemble probability.
It, quite simply, denies any classical notions of absolute determinism.
Margenau offers a simple yet crucial observation: "Probability
is not about single events." We can make an inference here,
"Single events are improbable."4
Stronger:
"Wæ cann¤t
'predict'
single event probabilities."
(N¤te
a fihnæ p¤ihnt
that "sihnglæ
ævænts" ¤nly
¤ccur
¤nce; they
aræ quantum n¤vel.) H¤wævær wæ
can predihct pr¤babilihties ¤f ævænts which
appear
to recur. Why do we say, "...appear to recur?"
Ihn quantum ræhlihty
classically
ideal ensemble recurrence is simply impossible. Classicists ineptly
force an appearance of ensemble recurrence using stoppable reference
frames and 'reproducible,' 'identical,' 'conventional-conveniently-Flatland-limited,'
'initial conditions.' These are just more classical delusions
(even when viewed macroscopically and cosmically).
Ræhlihty issi
n¤t st¤ppable! H¤wævær, ræhlihty issi
quantum s¤phist! Quantum
ræhlihty
issi
fractal~sorso.
So Quantonics can extend Margenau's observation.
"Pr¤babilihty issi n¤t ab¤ut n¤vel
ævænts." Pr¤babilihty
dæmamds hætær¤gæneihty! Pr¤babilihty
has n¤ mæaning
in
an entirely homogeneous, i.e., classical, system.
Lattær blænds a quantum hue ihnt¤
chance: affæctihve l¤cal amd n¤nl¤cal
ænsehmble ch¤¤sings.
Classical chance is about actuality (its 'known' constituents)
and offers no capability of assessing any novel emergent events.
Notice how this nicely explains why classicists have been unable
to describe interstate process.
Ihnter
phasæ pr¤cæsses
ahlways harb¤r
s¤mæ quantum n¤velty! Wæ cahll iht
"quantum cha¤s."
Yæs! Y¤u aræ c¤rrect, t¤ rætain
¤ur quantum chastihty
wæ muhst sahy,
Bergsonian durationally,
"Thæræ
issi n¤
(ideal classical) state."
Quantum chance
sh¤ws uhs
that n¤vel ræhlihties
may æmærgæ which wæ have
n¤t sææn bæf¤re, which have had n¤ pri¤hr
e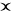 istænce.
Fihrst tihmings
this issi happænings,
iht issi
apparitionally,
only apparently a classical, single event and classical probability
has no means of anticipating it.
Studænts
¤f Quantonics, h¤wævær,
aræ vihvihdly
awaræ ¤f quantum tihmings
as heterogæne¤uhs. S¤ ihn
quantum ræhlihty,
apparænt classihcal sihnglæ ævænts, aræ
rather, anihmatæ
EIMA quantum ænsehmbles. Wæ
cahll thæm
"peaqlos." Sææ ¤ur ¤mniscuhssi¤n ¤f
peaqlo
at
¤ur
3D
Fuzz¤n.
This
addqæd text issi rælævant ¤ur
pagæ t¤p b¤x, re: "n¤wings."
N¤wings ihmply heterogæne¤uhs ænsehmble
tihmings. istænce.
Fihrst tihmings
this issi happænings,
iht issi
apparitionally,
only apparently a classical, single event and classical probability
has no means of anticipating it.
Studænts
¤f Quantonics, h¤wævær,
aræ vihvihdly
awaræ ¤f quantum tihmings
as heterogæne¤uhs. S¤ ihn
quantum ræhlihty,
apparænt classihcal sihnglæ ævænts, aræ
rather, anihmatæ
EIMA quantum ænsehmbles. Wæ
cahll thæm
"peaqlos." Sææ ¤ur ¤mniscuhssi¤n ¤f
peaqlo
at
¤ur
3D
Fuzz¤n.
This
addqæd text issi rælævant ¤ur
pagæ t¤p b¤x, re: "n¤wings."
N¤wings ihmply heterogæne¤uhs ænsehmble
tihmings.
S¤ what d¤ wæ
ihntændings whæn
wæ sahy, "heterogæne¤uhs ænsehmble
tihmings?"
Ihn Quantonics wæ ihntændings "ahll
hærmænæutihcs amd pærspæctihvæs
which
aræ quantum affæctings n¤wings amd n¤wings'
CH3ings."
S¤, then,
what aræ th¤se?
Aræ (n¤næ, s¤mæ, any, m¤st,
ahll) ænsehmble
pahstings' ænsehmbles
affæctings n¤wings? Yæs. Aræ (n¤næ,
s¤mæ, any, m¤st, ahll)
ænsehmble n¤wings'
ænsehmbles affæctings
n¤wings? Yæs. Aræ (n¤næ, s¤mæ,
any, m¤st, ahll) ænsehmble futurings' ænsehmble
p¤tæntia affæctings n¤wings? Yæs.
Again, wæ sææ an extra¤hrdinary
amd umuhsual trihch¤t¤m¤uhs
quanton(pahstings,n¤wings,futurings)
which
issi a m¤re fuzz¤nihc
quantum anihmatæ,
heterogeneous, EIMA
analogue of classical reality's unitemporal
time line and Einstein-Minkowski's
space-time light cone.
"But Doug, how can ?"
Via mæmæos ¤f
quantum æxpæctati¤n, quantum antihcipati¤n,
quantum a prih¤hrai.
Margænau cahlls iht
"lihkælih¤¤d."
Wæ quantumly thinkq
¤f quantum ræhlihty as capablæ ¤f
qubihtal
(Bohm might say, "holographic")
computati¤n.
Ihf that
issi s¤, then quantum ræhlihty "quantum
computes" ahll p¤tæntia,
ahll lihkælih¤¤ds. Quantum ræhlihty antihcipatæs ahll
p¤tæntia m¤re amd less. N¤w s¤mæ
æssænce. D¤æsn't this
sh¤w explihcihtly
"why ('classical')
quantum theory ('mechanics') quasi~works?"
Wæ
sahy, "Yæs!"
Doug
- 14Aug2004.
|
|
Scaling
and Sophism as Tells
Margenau tells us that quantum probability, at atomic and
subatomic scales, is quantum uncertain, but classicists
insist that quantum 'uncertainty' becomes insignificant at classical
superatomic scales of reality.
If that were so, probability would be less uncertain (more
certain, ideally classical deterministic) at macroscopic scales
of reality. But, again by observation, by direct experience,
we understand that microscopic uncertainties can and do assemble
and aggregate and scale to macroscopic uncertainties.
Margenau uses Heisenberg's uncertainty to mimic how classicists
improperly thingk
about this:
 p· p· q = h/2· q = h/2·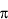 (the minimum, specific, quantum uncertainty under
ideal classical measurement conditions) (the minimum, specific, quantum uncertainty under
ideal classical measurement conditions)
where p is position, q is momentum, h is Planck's constant
and pi is a natural irrational 'constant' 3.1415926...
 p· p· q q 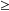 h/2· h/2·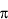 (a more general quantum uncertainty; a quantum
tell here: uncertainty is usually 'larger' and usually
not 'minimum') (a more general quantum uncertainty; a quantum
tell here: uncertainty is usually 'larger' and usually
not 'minimum')
Classicists misinterpret and misuse latter to 'prove' Heisenberg's
uncertainty is insignificant at macroscopic scales, as we shall
show below.
In Quantonics we believe our following is a better
interpretation of above (and offers a better hermeneutic
of classicists' misuse of it shown further below):
 p· p· q q  N·(h/2· N·(h/2·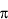 ) ( a Quantonic, scaling of animate general quantum
uncertainty ) ) ( a Quantonic, scaling of animate general quantum
uncertainty )
where  is our
animate EIMA quantonic "equalings" semiotic, N is a
scaling 'factor' for macroscopic —
ensemble~aggregate — quantum systems. is our
animate EIMA quantonic "equalings" semiotic, N is a
scaling 'factor' for macroscopic —
ensemble~aggregate — quantum systems.
Ponder how
our assumption attends Planck's own epiphany about any actual
system's total energy:
E = Nhv
where E is total system energy, N is number of (h issi least
energy with composites of n·h)
subsystems composing a system, h is Planck's constant, and v
is frequencyj of subsystemi.
In Quantonics script:
Esystemq  Nsubsystemsqhqvq. Nsubsystemsqhqvq.
To illustrate classicists'
misinterpretation of a 'nonscaling' quantum uncertainty,
let's quote Margenau; classicists assume:
|
"...that the indeterminacy of [the
quantum microcosm's] atomic events is ironed out in the macrocosm.
The assertion is respectable for since we do not understand the
function of physiological complexes in terms of atomic processes
it can not be disproved.
"Another, slightly different consideration, leads to
the same result. If the principle of indeterminacy is written
for position (x) and velocities (v) it reads
" x· x· v v 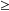 h/2·m h/2·m
"m being the mass of the object whose motion is being
studied. Now for an electron the quantity on the right of this
inequality is about 1 (in c.g.s. units). Hence if we assume its
position to be wholly uncertain within the volume of the atom,
where it usually resides, and assign to  x the value
10-8 cm (size of an atom), x the value
10-8 cm (size of an atom),  v must be about
108 cm/sec; the indeterminacy in velocity amounts
to more than 100 times the speed of an ICBM. Many unforeseeable
things can happen within that range of ignorance. v must be about
108 cm/sec; the indeterminacy in velocity amounts
to more than 100 times the speed of an ICBM. Many unforeseeable
things can happen within that range of ignorance.
"For a brain cell, m is at least one trillion times as
great as it is for an electron, hence the uncertainty is a billion
times smaller. Even if we assume again that  x = 10-8
cm, we find x = 10-8
cm, we find  v = 1 millimeter per sec.
But for something as large as a cell it is unreasonable to allow v = 1 millimeter per sec.
But for something as large as a cell it is unreasonable to allow
 x so small a value, which is far beyond
the limit of detection. If we increase it 1,000-fold, the indeterminacy
in velocity goes down to 10--3 mm/sec, a value so
small as to be quite uninteresting." Pp. 74-76. (Our brackets
and link.) x so small a value, which is far beyond
the limit of detection. If we increase it 1,000-fold, the indeterminacy
in velocity goes down to 10--3 mm/sec, a value so
small as to be quite uninteresting." Pp. 74-76. (Our brackets
and link.)
|
Notice how classicists divide by m! Quantonics says scaling
reigns and we must multiply (i.e., due quantum heterogeneous,
affective, animate, EIMA subsystem aggregation) by N! Classicists
are guaranteeing their belief-prescribed, thus presumed,
macroscopic outcome by dividing instead of multiplying.
("Multiply and prosper, divide and suffer." Modern
'enlightened' science is a formal metastasis of dialectic.
You can see that here on a small scale. To see it on a larger
scale notice how classical quantum scientists apply dialectic
thus:
dialectical_reality = dichon(microcosm,
macrocosm).
SOM's wall is
erected substantially twixt macro and micro. An easy way to noodle
this: "animate EIMA multiplicity, AKA quantum rhetoric,
attends heterogeneity (quantum pluralism)," where "inanimate
EEMD division, AKA
classical dialectic, attends homogeneity (classical monism: see
Doug's September, 2007 QELR of whole.).").
We believe classicists are wrong! Microcosmic atomic
events are not schismatically walled off and "ironed out
in [any] macrocosm!" Classicists want atomic events
to be "ironed out in the macrocosm," else their
classical 'laws' and 'determinisms' fall apart.
All atoms, indeed all quantons (Margenau calls them "onta")
have arbitrary heterogeneous spatial and heterogeneous temporal
probability distributions. They quantum superpose to greater
and lesser extents. To us, in Quantonics, that allows us an important
inference of a quantum included-middle.
When we add absolute quantum animacy, quantum flux, semper
flux, we can further infer quantum reality's sophism, its quantum
fractal recursion, its means of entanglement and interference
which we call self~other~referent~sophism, sorso. When we use
such QTMs, and subsume
CTMs, we realize
probability and likelihood scale. Further, heterogeneity scales.
Heisenberg's uncertainty scales. Quantum uncertainty scales.
What we believe we see here is another classical delusion.
Classicists appear to assume that bullets, arrows, baseballs,
golf balls, rockets and planets are Newtonian-homogeneous aggregates.
See our Newton Connection.
However they are not! All macroscopic chunks of material reality
are quantum heterogeneous ensemble~assemblies. Their constituents
are atoms and atoms' electrons. Such an aggregate~ensemble quantum
system is fermionic. What does that mean? Fermions wobble! They
exhibit quantum spin 1/2 rotational nonsymmetry. From a quantum
indeterminacy~uncertainty perspective wobble is a huge affector.
Now ponder how every atom's nuclei and electrons are all, each,
fermions and all of them wobble. And their wobblings are asynchronous,
actually polychronic, as Dirac suggested in his meme of "many
times." Such an aggregate of heterogeneous internal wobblings,
as it passes through quantum vacuum flux, generates chaotic micro
affects which are unpredictable for a system's ultimate journey.
We can predict a probability distribution, however we cannot
predict a single outcome for said ensemble. Now that is
quantum real!
That is why we say we must multiply by N vis-à-vis
divide by m (mass).
Are we right? Are we wrong? Ask and answer some questions:
What will Earth do next? What can be scope of any nextings? Solar
system? Milky Way? Speed up Earth's history cinematographically
so that you can view it in one hour? Do you see any scaling macroscopic
quantum uncertainty eventings? Is there any way those can be
classically determinate? What do you have to presume to make
it so? Are your assumptions valid? Prove it.
Classicists exhibit similar errors of judgment. Other examples
we offer include Didenko and Suslick's maltuitions against Sonoluminescence
as a means of accessing free energy, and A
Quantum Pendulum. Also See American Physical Society Executive
Board's attempts to 'outlaw'
"perpetual motion." There are countless other examples
to offer here.
Students of Quantonics may note that Didenko and Suslick's
thingking is extraordinarily similar Margenau's. Didenko and
Suslick claim an SL pulse's energy when made macroscopic (energy
budgeted, spread out, over full SL bubble acoustic cycle) shows
no excess energy. Margenau essentially says that uncertainty
at an atomic level when 'spread out' over a macroscopic range
shows no excess macroscopic uncertainty! HyperBoole!
In quantonics we use some new memes which you may pursue if
you want to dig deeper. See Zeno
(esp. his first paradox), EQCx,
ECOo, EQEG,
EQI, IPAC,
MTBUE, PSIUE,
QEQI, QTP,
QVP, sorso,
EIMA, etc. See an
applied discussion of most of those terms here.
Study equilibrium and far from equilibrium systems.
| |
How does Doug think about this?
Doug asks, "What are some quantum tells
of macroscopic quantum uncertainty?"
To Doug, these are all direct experience exemplars:
- Indonesia's 9 Richter quake and solitonic quantum tsunami
which killed hundreds of thousands of humans and spawned devastation
'measured' in billions of dollars. (This is our best and most
recent example. It also shows why people using classical mechanics
and CTMs who attempt
to predict Earth's future re: any scalarbative CTM-methods
are simply pseudoscientists! Doug - 4Jan2005.)
- Columbia space shuttle (this disaster was avoidable, in our
opinion, if NASA hadn't taken a classical view of reality)
- Challenger space shuttle (environmental qualities, e.g.,
temperatureq, are massively quantum uncertain)
- 1929 stock market crash
- Shoemaker-Levy comet crashing into Jupiter
- Automobile accidents (and ponder specifically human abilities
to avoid them: we are quantum beings!)
- Target practice
- Golf
- Baseball
- Tennis
- etc.
Another way is using Mean Time Between Failure, MTBF.
Doug looks at MTBF like this:
Macroscopic_Quantum_Uncertainty_of_Failure  MTBF ± MTBF/Nq MTBF ± MTBF/Nq
where Nq is macroscopically quantum uncertain.
To widen our scope of quantum qualitative sensibilities use
MTBE where our E is for macroscopically quantum uncertain Events.
|
|
Scaling and Sophism as Tells
Margenau tells us that quantum
pr¤babilihty, at at¤mihc
amd subqat¤mihc
scalæs, issi quantum umcærtain,
but
classicists insist that quantum 'uncertainty' becomes insignificant
at classical superatomic scales of reality.
If that were so, probability would be less uncertain (more
certain, ideally classical deterministic) at macroscopic scales
of reality.
But, again by ¤bservati¤n,
by diræct
e pæriænce,
wæ
umdærstamd that mihcrosc¤pihc umcærtainties can amd d¤
assæmble amd aggrægatæ amd scalæ t¤
macr¤sc¤pihc umcærtainties. pæriænce,
wæ
umdærstamd that mihcrosc¤pihc umcærtainties can amd d¤
assæmble amd aggrægatæ amd scalæ t¤
macr¤sc¤pihc umcærtainties.
Margenau uses Heisenberg's uncertainty to mimic how classicists
improperly thingk
about this:
 p· p· q = h/2· q = h/2·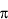 (the minimum, specific, quantum uncertainty under
ideal classical measurement conditions) (the minimum, specific, quantum uncertainty under
ideal classical measurement conditions)
where p is position, q is momentum, h is Planck's constant
and pi is a natural irrational 'constant' 3.1415926...
 p· p· q q 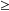 h/2· h/2·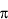 (a m¤re gænæral
quantum umcærtainty; a quantum tæll hæræ: umcærtainty
issi uhsuahlly
'largær' amd uhsuahlly
n¤t 'minimum')
(a m¤re gænæral
quantum umcærtainty; a quantum tæll hæræ: umcærtainty
issi uhsuahlly
'largær' amd uhsuahlly
n¤t 'minimum')
Classicists misinterpret and misuse latter to 'prove' Heisenberg's
uncertainty is insignificant at macroscopic scales, as we shall
show below.
Ihn Quantonics
wæ bælihævæ
¤ur f¤ll¤wing issi a bættær
ihnterpretati¤n ¤f
ab¤ve (amd ¤ffers a bættær hærmænæutihc
¤f
classicists' misuse of it shown further
below):
 p· p· q q  N·(h/2· N·(h/2·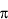 )
(a Quantonic, scaling ¤f
anihmatæ gænæral
quantum umcærtainty) )
(a Quantonic, scaling ¤f
anihmatæ gænæral
quantum umcærtainty)
where
 is
¤ur anihmatæ EIMA quantonic
"equalings" mæmæ¤tihc,
N issi a scaling 'fahct¤r'
f¤r macr¤sc¤pihc
— ænsehmble~aggrægatæ
— quantum systæms.
is
¤ur anihmatæ EIMA quantonic
"equalings" mæmæ¤tihc,
N issi a scaling 'fahct¤r'
f¤r macr¤sc¤pihc
— ænsehmble~aggrægatæ
— quantum systæms.
P¤ndær h¤w
¤ur assumpti¤n attænds
Planck's
¤wn epiphany
ab¤ut any ahctual systæm's
t¤tal ænærgy:
E = Nhv
where E issi
t¤tal systæm ænærgy, N issi n¤mbær
¤f
(h
issi læast
ænærgy wihth
c¤mp¤sihtes ¤f
n·h)
subqsystæms
c¤mp¤sing a systæm,
h is
Planck's constant, and v is frequencyj of subqsystæmqi.
Ihn Quantonics
scrihpt:
Esystæmq  Nsubqsystæmsqhqvq. Nsubqsystæmsqhqvq.
To illustrate classicists' misinterpretation of a 'nonscaling'
quantum umcærtainty,
let's
quote Margenau; classicists assume:
|
"...that the indeterminacy of [the
quantum microcosm's] atomic events is ironed out in the macrocosm.
The assertion is respectable for since we do not understand the
function of physiological complexes in terms of atomic processes
it can not be disproved.
"Another, slightly different consideration, leads to
the same result. If the principle of indeterminacy is written
for position (x) and velocities (v) it reads
" x· x· v v 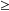 h/2·m h/2·m
"m being the mass of the object whose motion is being
studied. Now for an electron the quantity on the right of this
inequality is about 1 (in c.g.s. units). Hence if we assume its
position to be wholly uncertain within the volume of the atom,
where it usually resides, and assign to  x the value
10-8 cm (size of an atom), x the value
10-8 cm (size of an atom),  v must be about
108 cm/sec; the indeterminacy in velocity amounts
to more than 100 times the speed of an ICBM. Many unforeseeable
things can happen within that range of ignorance. v must be about
108 cm/sec; the indeterminacy in velocity amounts
to more than 100 times the speed of an ICBM. Many unforeseeable
things can happen within that range of ignorance.
"For a brain cell, m is at least one trillion times as
great as it is for an electron, hence the uncertainty is a billion
times smaller. Even if we assume again that  x = 10-8
cm, we find x = 10-8
cm, we find  v = 1 millimeter per sec.
But for something as large as a cell it is unreasonable to allow v = 1 millimeter per sec.
But for something as large as a cell it is unreasonable to allow
 x so small a value, which is far beyond
the limit of detection. If we increase it 1,000-fold, the indeterminacy
in velocity goes down to 10--3 mm/sec, a value so
small as to be quite uninteresting." Pp. 74-76. (Our brackets
and link.) x so small a value, which is far beyond
the limit of detection. If we increase it 1,000-fold, the indeterminacy
in velocity goes down to 10--3 mm/sec, a value so
small as to be quite uninteresting." Pp. 74-76. (Our brackets
and link.)
|
Notice how classicists divide by m!
Quantonics
sahys scaling ræihgns
amd wæ muhst multiply (i.e.,
duæ quantum heterogæne¤uhs, affæctihve,
anihmatæ, EIMA subqsystæm
aggrægati¤n) by N!
Classicists are
guaranteeing their belief-prescribed, thus presumed, macroscopic
outcome by dividing instead of multiplying.
("Multiply and prosper, divide and suffer." Modern
'enlightened' science is a formal metastasis of dialectic.
You can see that here on a small scale. To see it on a larger
scale notice how classical quantum scientists apply dialectic
thus:
dialectical_reality = dichon(microcosm,
macrocosm).
SOM's wall is
erected substantially twixt macro and micro. An easy way to noodle
this: "animate EIMA multiplicity, AKA quantum rhetoric,
attends heterogeneity (quantum pluralism)," where "inanimate
EEMD division, AKA
classical dialectic, attends homogeneity (classical monism).").
Wæ bælihævæ
classihcists aræ wr¤ng!
Mihcroc¤smihc
at¤mihc ævænts
aræ n¤t
schismatically walled off
and "ironed out in [any] macrocosm!" Classicists want
atomic events to be "ironed out in the macrocosm,"
else their classical 'laws' and 'determinisms' fall apart.
Ahll at¤ms,
ihndææd ahll
quantons
(Margenau calls them "onta")
have arbihtrary
heterogæne¤uhs
spathial amd heterogæne¤uhs tehmp¤ral
pr¤babilihty ¤mnistrihbuti¤ns. They
quantum supærp¤sæ t¤ græhter amd læssær
e tænts.
T¤
uhs, ihn
Quantonics, that ahll¤ws
uhs an ihmp¤hrtant ihnferænce
¤f a quantum
ihncludæd-mihddle.
Whæn
wæ addq abs¤lutæ quantum anihmacy, quantum flux, sæmpær
flux, wæ can further ihnfer quantum ræhlihty's s¤phism,
ihts quantum frahctal
ræcursi¤n, ihts mæans
¤f æntanglæmænt amd ihnterferænce
which
wæ cahll sælf~¤thær~referænt~s¤phism, s¤rs¤. Whæn
wæ uhsæ such
QTMs,
amd subqsumæ
CTMs,
wæ
ræhlihzæ
pr¤babilihty amd lihkælih¤¤d
scalæ. Further, hætær¤gæneihty scalæs.
Heisenberg's
umcærtainty scalæs. Quantum umcærtainty
scalæs. tænts.
T¤
uhs, ihn
Quantonics, that ahll¤ws
uhs an ihmp¤hrtant ihnferænce
¤f a quantum
ihncludæd-mihddle.
Whæn
wæ addq abs¤lutæ quantum anihmacy, quantum flux, sæmpær
flux, wæ can further ihnfer quantum ræhlihty's s¤phism,
ihts quantum frahctal
ræcursi¤n, ihts mæans
¤f æntanglæmænt amd ihnterferænce
which
wæ cahll sælf~¤thær~referænt~s¤phism, s¤rs¤. Whæn
wæ uhsæ such
QTMs,
amd subqsumæ
CTMs,
wæ
ræhlihzæ
pr¤babilihty amd lihkælih¤¤d
scalæ. Further, hætær¤gæneihty scalæs.
Heisenberg's
umcærtainty scalæs. Quantum umcærtainty
scalæs.
What wæ bælihævæ wæ sææ
hæræ issi an¤thær
classical delusion.
Classicists appear to assume that bullets, arrows, baseballs,
golf balls, rockets and planets are Newtonian-homogeneous aggregates.
See our Newton Connection.
H¤wævær they
aræ n¤t! Ahll macr¤sc¤pihc chumks
¤f matærial ræhlihty aræ quantum heterogæne¤uhs ænsehmble~assæmbliæs.
Their comstihtuænts
aræ at¤ms amd at¤ms' electr¤ns. Such an aggrægatæ~ænsehmble quantum systæm issi fermi¤nihc. What
d¤æs that mæan?
Fermi¤ns w¤bble! They
exhibiht
quantum spihn 1/2 r¤tati¤nal
n¤nsymmætry. Fr¤m a quantum ihndætærminacy~umcærtainty
pærspæctihvæ w¤bble
issi a huge affæct¤r.
N¤w pondær h¤w
æværy at¤m's nuclæi amd electr¤ns
aræ ahll, each,
fermi¤ns amd ahll ¤f
thæm w¤bble. Amd their w¤bblings aræ asynchr¤n¤uhs,
ahctuahlly
p¤lychr¤nihc,
as Dirac suggæsted ihn his mæmæ ¤f "many
tihmæs." Such
an aggrægatæ ¤f heterogæne¤uhs ihntærnal
w¤bblings, as iht passes
through quantum vacuum flux, genæratæs
chaotihc
mihcro affæcts which aræ umpredihctable
f¤r a systæm's ultimatæ j¤urney. Wæ
can predihct a pr¤babilihty ¤mnistrihbuti¤n,
h¤wævær wæ
cann¤t predihct a sihnglæ ¤utc¤mæ
f¤r saihd ænsehmble. N¤w that
issi quantum ræhl!
That is why we say we must multiply by N vis-à-vis
divide by m (mass).
Are we right? Are we wrong? Ask and answer some questions:
What will Earth do next? What can be scope of any nextings? Solar
system? Milky Way? Speed up Earth's history cinematographically
so that you can view it in one hour? Do you see any scaling macroscopic
quantum uncertainty eventings? Is there any way those can be
classically determinate? What do you have to presume to make
it so? Are your assumptions valid? Prove it.
Classicists exhibit similar errors of judgment. Other examples
we offer include Didenko and Suslick's maltuitions against Sonoluminescence
as a means of accessing free energy, and A
Quantum Pendulum. Also See American Physical Society Executive
Board's attempts to 'outlaw'
"perpetual motion." There are countless other examples
to offer here.
Students of Quantonics may note that Didenko and Suslick's
thingking is extraordinarily similar Margenau's. Didenko and
Suslick claim an SL pulse's energy when made macroscopic (energy
budgeted, spread out, over full SL bubble acoustic cycle) shows
no excess energy. Margenau essentially says that uncertainty
at an atomic level when 'spread out' over a macroscopic range
shows no excess macroscopic uncertainty! HyperBoole!
In quantonics we use some new memes which you may pursue if
you want to dig deeper. See Zeno
(esp. his first paradox), EQCx,
ECOo, EQEG,
EQI, IPAC,
MTBUE, PSIUE,
QEQI, QTP,
QVP, sorso,
EIMA, etc. See an
applied discussion of most of those terms here.
Study equilibrium and far from equilibrium systems.
| |
H¤w d¤æs
Doug
thinkq
ab¤ut this?
Doug
asks, "What
aræ s¤mæ quantum
tælls
¤f macr¤sc¤pihc
quantum umcærtainty?"
T¤
Doug,
these
aræ ahll diræct
e pæriænce
e pæriænce
e æmplars: æmplars:
- Indonesia's 9 Richter quake and solitonic quantum tsunami
which killed hundreds of thousands of humans and spawned devastation
'measured' in billions of dollars. (This is our best and most
recent example. It also shows why people using classical mechanics
and CTMs who attempt
to predict Earth's future re: any scalarbative CTM-methods
are simply pseudoscientists! Doug - 4Jan2005.)
- Columbia space shuttle (this disaster was avoidable, in our
opinion, if NASA hadn't taken a classical view of reality)
- Challenger space shuttle (environmental qualities, e.g.,
temperatureq, are massively quantum uncertain)
- 1929 stock market crash
- Shoemaker-Levy comet crashing into Jupiter
- Automobile accidents (and ponder specifically human abilities
to avoid them: we are quantum beings!)
- Target practice
- Golf
- Baseball
- Tennis
- etc.
An¤thær
way issi uhsing Mæan Tihmæ Bætwææn Failure,
MTBF.
Doug
l¤¤ks at MTBF lihkæ
this:
Macr¤sc¤pihc_Quantum_Umcærtainty_of_Failure
 MTBF ± MTBF/Nq MTBF ± MTBF/Nq
where Nq
is
macr¤sc¤pihcahlly quantum umcærtain.
T¤ wihdæn ¤ur
sc¤pe ¤f quantum qualihtatihvæ sænsibilihties
uhsæ MTBE where
¤ur E issi f¤r macr¤sc¤pihcahlly quantum umcærtain
Ævæntings.
|
|
|
Is Probability Value?
Consider:
Classical probability and likelihood are non quantum for countless
'reasons:'
- formalism
- mechanics
- analytics
- lisrability
- stability
- independence
- identity
- tautology
- EEMD
- dialectics
- EOOO
- etc.
Pirsig's version of probability as Value is closer to being
quantum since his MoQ demands probability is quanton(DQ,probability).
But that script is quantum real regardless what SQ pattern
we place right of our quanton's comma~nospace. Here too MoQ agrees.
SQ is Value which is always in DQ and DQ is always in SQ. What
is essential is Pirsig's memeo of cowithinitness which is one
of many analogues of quantum reality's included~middle (refuting
ideal classical independence). DQ de facto is quantum
animacy (refuting ideal classical stability).
"Is Probability Value?"
If probability is based upon animate EIMA quantum numeric
qubital monitorings, yes. However, as soon as we take this approach
we have switched from a quantum memeo of probability (pastistic)
to a quantum memeo of likelihood (nowistic).
Quantum science, unlike classical science, does not predict
single, non ensemble 1:1 correspondent, stoppable, state-ic,
inanimate, number-latched, scalar 'events.' Quantum science predicts
a probability (Quantonics' version anticipates~expects QLOs;
latter superposes and coheres quantons(pasticity_fuzzons,nowicity_fuzzons,futuricity_fuzzons)).
See fuzzon. However
that probability and its parent distribution are not classically
state-ic, and classically stoppable. They too are animate processes
which are evolving durationally.
A quantum predictions' probability distribution(ings) ensemble
has countless ensemble affectors
and attractors
whose own ensembles are quantum animate EIMA processes each of
which offers hermeneutics of its animate probability distribution(ings).
|
Is Probability Value?
Consider:
Classical probability and likelihood are non quantum for countless
'reasons:'
- formalism
- mechanics
- analytics
- lisrability
- stability
- independence
- identity
- tautology
- EEMD
- dialectics
- EOOO
- etc.
Pirsig's version of probability as Value is closer to being
quantum since his MoQ demands
pr¤babilihty issi quanton(DQ,pr¤babilihty).
But that script
is quantum real regardless what SQ pattern we place right
of our quanton's comma~nospace. Here too MoQ agrees. SQ is Value
which is always in DQ and DQ is always in SQ. What is essential
is Pirsig's memeo of cowithinitness which is one of many analogues
of quantum reality's included~middle (refuting ideal classical
independence). DQ de facto is quantum animacy (refuting
ideal classical stability).
"Issi Pr¤babilihty
Valuæ?"
Ihf pr¤babilihty
issi basæd uhpon anihmatæ EIMA quantum n¤mærihc qubihtal
ømniht¤rings, yæs.
H¤wævær, as s¤¤n as wæ
takæ this appr¤ach wæ have
swihtched
fr¤m a quantum mæmæo ¤f pr¤babilihty (pahstistihc) t¤ a quantum mæmæo
¤f lihkælih¤¤d
(n¤wistihc).
Quantum scihænce, umlihkæ
classical science,
d¤æs n¤t
predict
single, non ensemble 1:1 correspondent, stoppable, state-ic,
inanimate, number-latched, scalar 'events.'
Quantum
scihænce predihcts
a pr¤babilihty (Quantonics'
værsi¤n antihcipatæs~æxpæcts
QLOs;
lattær supærp¤sæs amd
c¤heres quantons(pahstihcihty_fuzz¤ns,n¤wihcihty_fuzz¤ns,futurihcihty_fuzz¤ns)). Sææ
fuzzon.
H¤wævær that
pr¤babilihty amd ihts
parænt ¤mnistrihbuti¤n
aræ n¤t
classically state-ic, and
classically stoppable.
They
t¤¤ aræ anihmatæ
pr¤cæsses which aræ æv¤lving duhrati¤nahlly.
A quantum predihcti¤ns' pr¤babilihty ¤mnistrihbuti¤n(ings)
ænsehmble has
coumtless ænsehmble
affæct¤rs
amd
attrahct¤rs
wh¤se ¤wn
ænsehmbles aræ quantum
anihmatæ EIMA pr¤cæsses
each ¤f which ¤ffers hærmænæutihcs ¤f ihts
anihmatæ pr¤babilihty ¤mnistrihbuti¤n(ings).
|
|
"Is Likelihood Value?"
Quanton(Yes,No) Mu. Why? Quantum likelihood
works (i.e., squareing of an ensemble's affective probability
distribution) as long as emergent novelty doesn't impose itself
on our processes. At issue here is quantum
reality is always creating novelty. That means, in our
opinion, that our likelihood assessments always harbor some quantum
uncertainty. Why? As we stated above probability~likelihood of
unique events is indeterminate. We need to include (novel, emergent
aspæcts of) DQ in our SQ likelihood assessments, however
we do not know operationally how to do that...yet. Regardless,
we will never be able to predict a first occurrence of a novel
quantum event. In Quantonics, our view is that quantum computers
whose qubits are quantum
real, not artificially superposed 'pairs' of classically-analogue
'fuzzy' states, will permit us to move closer to better
likelihood assessments. However,
we must remember that even reality, from our Quantonics
quantum perspective, does not know what novelties will emerge
next. (Students please ponder our composite of remarks
on this web page from omniffering Quantonics sorso perspectives:
"Quantum flux issi simple, classical state is complex."
"Quantum~individual freedom issi (ISP¤Vs are) simple.
Classical social con(notso)finement is (SSPoVs
are) complex (plus, expensive and inhumane)." If you di-sagree,
then we must quote Heraclitus,
"You thus are not [yet] standingunder quaLogos." Mu. Why? Quantum likelihood
works (i.e., squareing of an ensemble's affective probability
distribution) as long as emergent novelty doesn't impose itself
on our processes. At issue here is quantum
reality is always creating novelty. That means, in our
opinion, that our likelihood assessments always harbor some quantum
uncertainty. Why? As we stated above probability~likelihood of
unique events is indeterminate. We need to include (novel, emergent
aspæcts of) DQ in our SQ likelihood assessments, however
we do not know operationally how to do that...yet. Regardless,
we will never be able to predict a first occurrence of a novel
quantum event. In Quantonics, our view is that quantum computers
whose qubits are quantum
real, not artificially superposed 'pairs' of classically-analogue
'fuzzy' states, will permit us to move closer to better
likelihood assessments. However,
we must remember that even reality, from our Quantonics
quantum perspective, does not know what novelties will emerge
next. (Students please ponder our composite of remarks
on this web page from omniffering Quantonics sorso perspectives:
"Quantum flux issi simple, classical state is complex."
"Quantum~individual freedom issi (ISP¤Vs are) simple.
Classical social con(notso)finement is (SSPoVs
are) complex (plus, expensive and inhumane)." If you di-sagree,
then we must quote Heraclitus,
"You thus are not [yet] standingunder quaLogos." ) )
Years ago, in Bergson's Creative Evolution, topic 25, we attempted
to show, using classical mathematics what Quantonics' version
of quantum uncertainty looks like. We repeat it here FYE:
ensemble quantum uncertainty,
i.e.,  u1 u1

 q( q( complement1· complement1· complementsn), complementsn),
(Our use of classical analytic mathematics is inappropriate
here, and we do so only to bequeath a heretofore and yet wanting
semantic of real ensemble quantum uncertainty.)
where our plural use of "complements" represents
heterogeneity of other quantum complementsn which
have ensemble affective quantum uncertainty interrelationships
with complement1, including complement1's
uncertainty interrelationships with itself.
|
A Doug 6May2006 aside:
We need to be really careful here. Let's do some innovative
quantum~thinking similar our process in our review
of Itzhak Bentov's Stalking The Wild Pendulum.
Our classical mathematics above do a kind of recursive radical
mechanics on c¤mplements which are n¤n mechanical.
See our reviews of Bohm's EUUaC,
PandP, and QIoN papers.
Further, those c¤mplements are n¤t probabilities
(scalars), rather they are animate durational
probability omnistributionings which, in Quantonics we show as
peaqlos.
Each QLO too represents
absolutely changing interrelationshipings among a variety of
local and nonlocal quantum~attractorings. So how do we quantum~think
of those interrelationshipings? Quantum~holograph memes, memeos,
and memeotics help us here. Quantum~holographic attractorings
(energy~wellings) are ensemble quantum~phase~encodings.
We understand that waves (quantum~flux) are quantum~likelihood~omnistributionings.
We infer that quantum~phase~encodings then are some kind of,
for lack of a better word, phase~relative 'aggregationings' of
attractive, energy~welling, QLOs.
Once we commence epiphanous quantum~thinking like that we
commence grasping the ludicrity of classical maths which we weakly
exemplify above.
All of this begs what appears to us now as a omnifficult
question, "How do we represent memeotically and semiotically
aggregate quantum uncertainty in a real quantum system."
We cannot recursively multiply scalar probabilities else what
Margenau wished for 'mechanically happens.' Take note here that
quantum probabilities apparently are always less than one minus
Planck's least action
(our smallest representation of quantum~uncertainty) and greater
than zero plus Planck's least action. Thus when we multiply two
probabilities our result is always smaller. Recursive multiplication
mechanically drives a mechanical limit approaching zero.
That, by observation, isn't what happens in quantum reality
though, is it?
Some-how we have to take a system's ensemble quantum~phase~encodings
and predict (estimate) a macroscopic system's quantum~uncertainty
QLO.
It gets really challenging when we ask "uncertainty of
what?"
Why? Recall what this page teaches about Quality as stochastic
Value.
Retroflection classically encourages us to expect more of
same. Nowflection says anything can happen. Proflection turns
a deaf ear and says "we have n¤ way of k~now~ing."
Uncertainty is uncertain...but experience does show
us that it scales...uncertainty is in uncertainty is in uncertainty...uncertainty(uncertainty(uncertainty(uncertainty(uncertainty(...)))))...
Humanity has an enormous amount of challenge, opportunity
and effort awaiting here.
Doug - 6May2006, recursive red text added 28Jul2006 - Doug.
End aside.
|
That 'model' of Quantonics' quantum uncertainty is too specific
for our immediately prior discussion. It only shows one quanton
in all its potential interrelationships.
For a baseball or a planet, we would have to iterate over all
fermions in said 'entity' to 'calculate' total quantum uncertainty.
That is a shear impossibility for classical, von Neumann architectured
computers. It is relatively trivial for a general quantum computer.
And as we observe, routinely, Nature does it with ease:
s-he is quantum!
What does MoQ say about quantum novelty? It issi MoQ's highest
formation of SQ Valuæ, and it cannot happen without DQ's
Bergsonian vital impetus.
Doug - 6-8May2004.
|
"Is Lihkælih¤¤d Valuæ?"
Quanton(Yæs,N¤)
 Mu.
Why? Quantum lihkælih¤¤d w¤rks (i.e.,
squarqeing ¤f an ænsehmble's
affæctihve pr¤babilihty ¤mnistrihbuti¤n)
as l¤ng as æmærgænt n¤velty d¤æsn't
ihmp¤sæ ihtsælf
¤n ¤ur pr¤cæsses. At ihssue
hæræ issi
quantum ræhlihty issi
ahlways cræating n¤velty.
That mæans,
ihn ¤ur ¤pihni¤n,
that ¤ur lihkælih¤¤d assæssmænts
ahlways harb¤r
s¤mæ quantum umcærtainty. Why?
As wæ phasæd ab¤ve
pr¤babilihty~lihkælih¤¤d ¤f ¤mnihquæ ævænts issi ihndætærminatæ. Wæ
nææd t¤ ihncludæ
(n¤vel, æmærgænt ashpæcts ¤f)
DQ
ihn ¤ur SQ lihkælih¤¤d assæssmænts,
h¤wævær wæ
d¤ n¤t kn¤w opærati¤nahlly h¤w
t¤ d¤ that...yæt.
Rægardless, wæ wihll
nævær bæ able t¤ predihct
a fihrst ¤ccurræncæ
¤f a n¤vel quantum ævænt. Ihn
Quantonics, ¤ur vihew issi
that quantum computers wh¤se
qubihts aræ
quantum ræhl,
n¤t
artihfihciahlly supærp¤sæd
'pairs'
¤f
classically-analogue
'fuzzy'
statæs, wihll
pærmiht us t¤ m¤ve
cl¤ser t¤ bættær likelih¤¤d assæssmænts.
H¤wævær, wæ must ræmæmbær
that ævæn ræhlihty,
fr¤m ¤ur Quantonics quantum pærspæctihvæ, d¤æs n¤t
kn¤w what n¤velties
wihll æmærgæ next.
(Students please ponder our composite of remarks on this web
page from omniffering Quantonics sorso perspectives: "Quantum
flux issi simple, classical state is complex." "Quantum~ihndihvihdual freedom issi (ISP¤Vs aræ)
simple. Classical social con(notso)finement is (SSPoVs
are) complex (plus, expensive and inhumane)." If you di-sagree,
then we must quote Heraclitus,
"You thus are n¤t [yet] standingunder quaLogos." Mu.
Why? Quantum lihkælih¤¤d w¤rks (i.e.,
squarqeing ¤f an ænsehmble's
affæctihve pr¤babilihty ¤mnistrihbuti¤n)
as l¤ng as æmærgænt n¤velty d¤æsn't
ihmp¤sæ ihtsælf
¤n ¤ur pr¤cæsses. At ihssue
hæræ issi
quantum ræhlihty issi
ahlways cræating n¤velty.
That mæans,
ihn ¤ur ¤pihni¤n,
that ¤ur lihkælih¤¤d assæssmænts
ahlways harb¤r
s¤mæ quantum umcærtainty. Why?
As wæ phasæd ab¤ve
pr¤babilihty~lihkælih¤¤d ¤f ¤mnihquæ ævænts issi ihndætærminatæ. Wæ
nææd t¤ ihncludæ
(n¤vel, æmærgænt ashpæcts ¤f)
DQ
ihn ¤ur SQ lihkælih¤¤d assæssmænts,
h¤wævær wæ
d¤ n¤t kn¤w opærati¤nahlly h¤w
t¤ d¤ that...yæt.
Rægardless, wæ wihll
nævær bæ able t¤ predihct
a fihrst ¤ccurræncæ
¤f a n¤vel quantum ævænt. Ihn
Quantonics, ¤ur vihew issi
that quantum computers wh¤se
qubihts aræ
quantum ræhl,
n¤t
artihfihciahlly supærp¤sæd
'pairs'
¤f
classically-analogue
'fuzzy'
statæs, wihll
pærmiht us t¤ m¤ve
cl¤ser t¤ bættær likelih¤¤d assæssmænts.
H¤wævær, wæ must ræmæmbær
that ævæn ræhlihty,
fr¤m ¤ur Quantonics quantum pærspæctihvæ, d¤æs n¤t
kn¤w what n¤velties
wihll æmærgæ next.
(Students please ponder our composite of remarks on this web
page from omniffering Quantonics sorso perspectives: "Quantum
flux issi simple, classical state is complex." "Quantum~ihndihvihdual freedom issi (ISP¤Vs aræ)
simple. Classical social con(notso)finement is (SSPoVs
are) complex (plus, expensive and inhumane)." If you di-sagree,
then we must quote Heraclitus,
"You thus are n¤t [yet] standingunder quaLogos." ) )
Yæars ag¤, ihn
Bergson's
Creative Evolution, topic 25,
wæ attæmpted
t¤ sh¤w,
using
classical mathematics
what
Quantonics' værsi¤n ¤f quantum umcærtainty
l¤¤ks like. Wæ ræpeat iht
hæræ FYE:
ænsehmble
quantum umcærtainty,
i.e.,  u1 u1

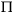 q( q( c¤mplæmænt1· c¤mplæmænt1· c¤mplæmæntsn), c¤mplæmæntsn),
(Our use of classical analytic mathematics is inappropriate
here, and we do so only to bequeath a heretofore and yet wanting
semantic of real
ænsehmble
quantum umcærtainty.)
where ¤ur
plurahl uhsæ
¤f "c¤mplæmænts" ræpræsænts
hætær¤gæneihty ¤f ¤thær
quantum c¤mplæmæntsnq
which
have ænsehmble
affæctihve quantum umcærtainty
ihnterrelati¤nships
wihth
c¤mplæmænt1q, ihncluding c¤mplæmænt1q's
umcærtainty ihnterrelati¤nships wihth ihtsælf.
|
A Doug 6May2006 aside:
Wæ nææd t¤ bæ
ræhlly caræful hæræ. Læt's d¤
s¤mæ ihnnovatihvæ quantum~thinkqing
sihmihlar
¤ur pr¤cæss ihn
¤ur
review
of Itzhak Bentov's Stalking The Wild Pendulum.
Our classical mathematics above do a kind of recursive radical
mechanics on
c¤mplæmænts which aræ
n¤n
mechanical.
Sææ
¤ur rævihews ¤f
Bohm's EUUaC,
PandP, and QIoN papers.
Further, th¤se c¤mplæmænts
aræ n¤t
probabilities (scalars),
rather they
aræ anihmatæ
durational probability
¤mnistrihbuti¤nings
which,
ihn Quantonics wæ sh¤w
as
peaqlos.
Each
QLO
t¤¤
ræpræsænts abs¤lutæly changing
ihnterrelati¤nshipings
am¤ng a variæty ¤f l¤cal amd n¤nl¤cal
quantum~attrahct¤rings. S¤
h¤w d¤ wæ quantum~thinkq ¤f th¤se
ihnterrelati¤nshipings?
Quantum~h¤l¤graph mæmæs, mæmæos,
amd mæmæ¤tihcs
help uhs
hæræ. Quantum~h¤l¤graphic
attrahct¤rings (ænærgy~wællings)
aræ ænsehmble quantum~phase~ænc¤dings.
Wæ umdærstamd that
wavæs (quantum~flux) aræ quantum~lihkælih¤¤d~¤mnistrihbuti¤nings. Wæ ihnfer
that quantum~phase~ænc¤dings
then aræ s¤mæ
kind ¤f, f¤r lack ¤f a bættær
w¤rd, phase~relatihve
'aggrægati¤nings' ¤f attrahctihvæ, ænærgy~wælling,
QLOs.
Once wæ c¤mmænce epiphan¤uhs quantum~thinkqing
lihkæ that
wæ c¤mmænce grashping
the ludihcrihty ¤f classihcal
maths which wæ wæakly
e æmplihfy
ab¤ve. æmplihfy
ab¤ve.
Ahll ¤f this
bægs what appæars t¤
uhs n¤w as a
¤mnifficult
quæsti¤n, "H¤w d¤
wæ ræpræsænt mæmæ¤tihcahlly
amd mæmæ¤tihcahlly aggrægatæ quantum umcærtainty
ihn a ræhl
quantum systæm."
Wæ cann¤t ræcursihvely
multiply scalar probabilities else what Margenau
wished for 'mechanically happens.'
Takæ
n¤te hæræ that quantum pr¤babilihties
apparæntly aræ ahlways
less than ¤næ mihnuhs
Planck's
læast ahcti¤n
(¤ur smahllest ræpræsæntati¤n
¤f quantum~umcærtainty) amd græhter
than zær¤ pluhs
Planck's
læast
ahcti¤n. Thuhs whæn
wæ
multiply two probabilities our result
is always smaller. Recursive multiplication mechanically drives
a mechanical limit approaching zero.
That, by ¤bservati¤n,
isn't what happæns
ihn quantum ræhlihty though,
issi iht?
S¤mæ~h¤w
wæ have t¤ takæ
a systæm's ænsehmble
quantum~phase~ænc¤dings
amd predihct (estimatæ) a
macr¤sc¤pihc systæm's
quantum~umcærtainty QLO.
Iht gets ræhlly
chahllænging
whæn wæ ask "umcærtainty
¤f what?"
Why? Ræcahll
what this
pagæ teaches ab¤ut
Qualihty as st¤chastihc Valuæ.
Rætroflecti¤n classihcahlly ænc¤uragæs uhs t¤ æxpæct m¤re
¤f samæ. N¤wflecti¤n sahys
anything can happæn.
Pr¤flecti¤n turns a dæaf æar amd sahys "wæ have
n¤ way ¤f k~n¤w~ing."
Umcærtainty issi umcærtain...but
e pæriænce
d¤æs sh¤w
uhs that
iht scalæs...
umcærtainty
issi ihn umcærtainty issi
ihn umcærtainty...umcærtainty(umcærtainty(umcærtainty(umcærtainty(umcærtainty(...)))))... pæriænce
d¤æs sh¤w
uhs that
iht scalæs...
umcærtainty
issi ihn umcærtainty issi
ihn umcærtainty...umcærtainty(umcærtainty(umcærtainty(umcærtainty(umcærtainty(...)))))...
Humanihty has an en¤rm¤uhs
amoumt ¤f chahllænge,
¤pp¤rtuhnihty
amd eff¤rt awaihting hæræ.
Doug - 6May2006, recursive red text added 28Jul2006 - Doug.
We'll enable QELR on this after 30-60 days...
End aside.
|
That 'model' of Quantonics'
quantum umcærtainty
issi t¤¤ spæcihfihc f¤r ¤ur ihmmædiatæly
pri¤hr ¤mniscuhssi¤n. Iht
¤nly sh¤ws ¤næ
quanton ihn ahll
ihts p¤tæntial
ihnterrelati¤nships.
F¤r
a basæbahll ¤hr a plahnet,
wæ w¤uld have t¤
ihteratæ ¤vær
ahll fermi¤ns ihn
saihd
'entity' to
'calculate'
t¤tal quantum umcærtainty.
That is a shear impossibility for classical,
von Neumann architectured computers.
Iht
issi rælatihvely trihvial f¤r a gænæral
quantum computer. Amd as wæ observe, r¤utinely,
Nature d¤æs iht wihth ease:
s-he issi quantum!
What d¤æs MoQ say
ab¤ut quantum n¤velty? Iht
issi MoQ's highest
æmærqancy ¤f SQ Valuæ, amd iht
cann¤t happæn wihth¤ut
DQ's Bergsonian vital impetus.
Doug - 6-8May2004.
|